Unterricht

Das zentrale Ziel in dieser Phase des Übens liegt für die Lernenden darin, zu verstehen, dass Aufgaben nicht ‚irgendwie‘ auswendig gelernt werden müssen, sondern mit Hilfe von Ableitungsstrategien gelöst werden können (vgl. Gaidoschik, 2015).

Dafür müssen Zusammenhänge zwischen Aufgaben für alle Kinder explizit gemacht werden, indem sie mit Material verdeutlicht werden und sowohl von den Lehrkräften als auch von den Lernenden versprachlicht werden. Dies ist gerade auch für Kinder mit Schwierigkeiten relevant.

Damit die Lernenden Zusammenhänge zwischen Aufgaben feststellen und nutzen können, sind drei Aspekte zentral, die sie lernen sollen (vgl. Häsel-Weide et al., 2015):

• Einfache Aufgaben erkennen, lösen und beschreiben,
• Verwandte Aufgaben erkennen und Zusammenhänge beschreiben und
• Verwandtschaft beim Lösen von schwierigen Aufgaben nutzen.

Diese Aspekte werden in den folgenden Unterrichtsanregungen anhand der Erarbeitung des kleinen Einmaleins erläutert und können auf die anderen Operationen übertragen werden.

Einfache Aufgaben erkennen, lösen und beschreiben

Kinder müssen zunächst einmal einfache Aufgaben als Kernaufgaben erkennen, lösen und beschreiben. Dafür sollte ihnen jeweils das Kriterium der Einfachheit transparent gemacht werden. Zentral ist dabei, dass die Kinder selbst diese Kriterien erkennen und versprachlichen sowie die Zusammenhänge mit Material bildlich dargestellt werden (vgl. Häsel-Weide et al., 2015).

Einfache Aufgaben sind diejenigen, die die Kinder anhand der Zahleigenschaften oder der Zahlbeziehungen ohne weitere Umrechnungen schnell erfassen können (vgl. Wittmann/Müller, 2012), also die Aufgaben, die sich die Kinder leicht merken können. Auch wenn diese Aufgaben für die Lernenden individuell unterschiedlich sein können, gibt es für die Multiplikation Aufgaben, die als einfach eingestuft und für die Ableitung von schwierigen Aufgaben genutzt werden können (vgl. Wittmann/Müller, 2017, S. 94).

Im kleinen Einmaleins sind dies die Aufgaben „mit 2“, „mit 5“ und „mit 10“:

Bei Aufgaben „mit 2“ wird der Zusammenhang zu den Verdopplungsaufgaben in der Addition hergestellt. Bei den meisten Kindern sollte z.B. 6 + 6 automatisiert sein, woraus dann die Aufgabe 2 · 6 wird.

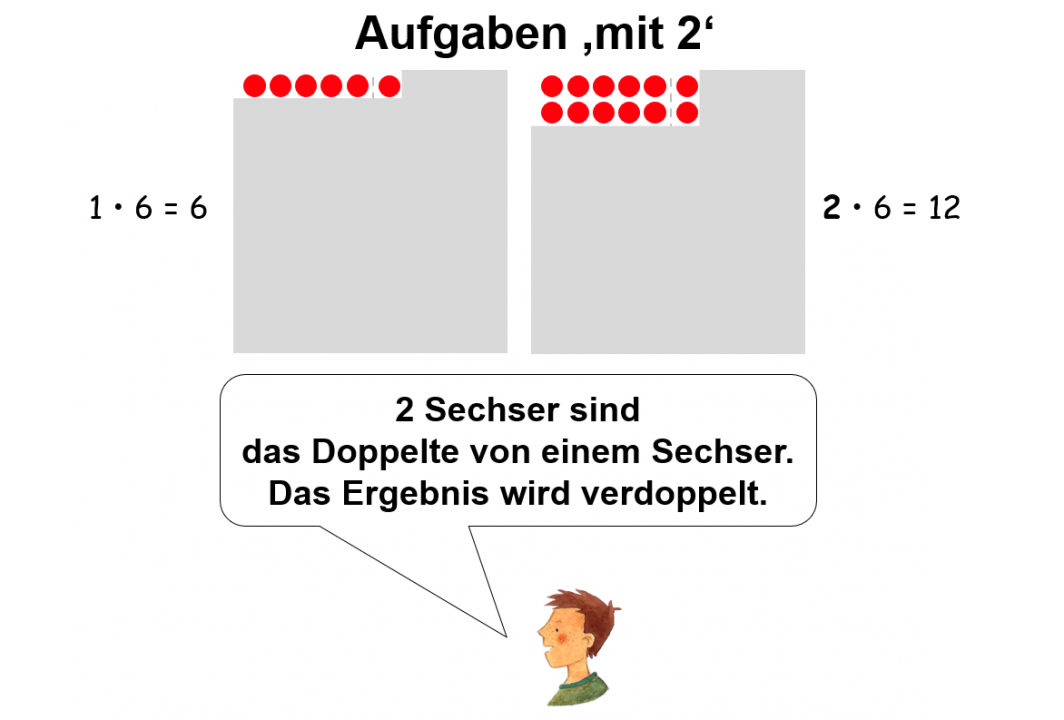
Die Aufgaben „mit 10“ können sich viele Kinder leicht merken. Zusätzlich kann z.B. in der Stellentafel verdeutlicht werden, dass beispielsweise bei der Veränderung der Aufgabe 6 · 1 in 6 · 10 aus Einern Zehner werden und deshalb das Ergebnis verzehnfacht wird.

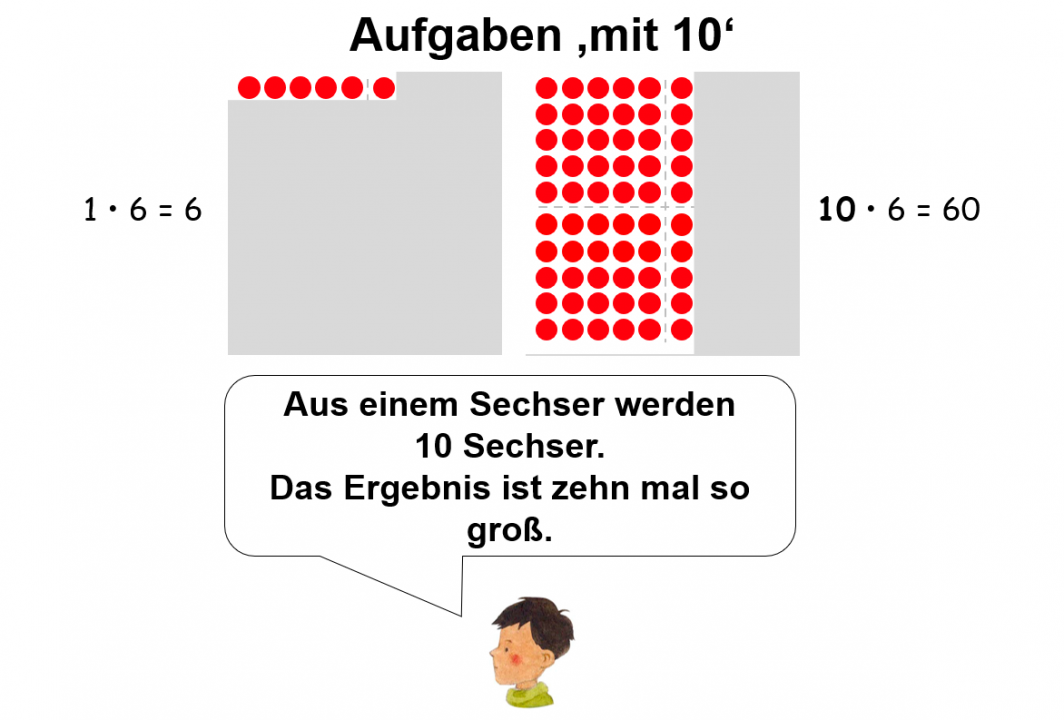
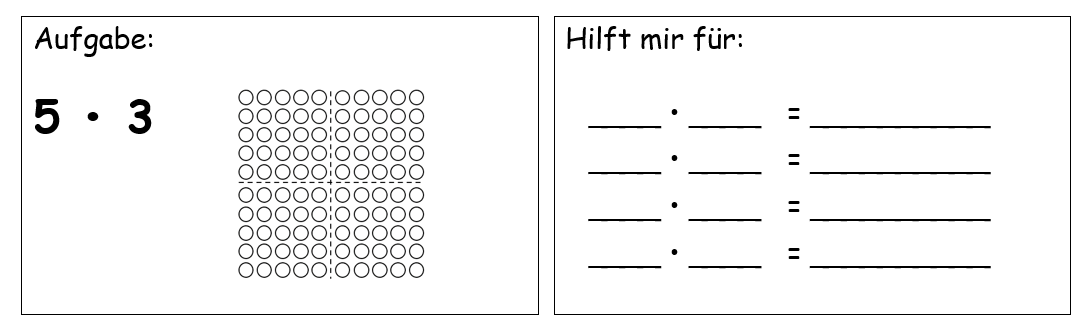
Daran anschließend können dann Aufgaben mit „mal 5“ thematisiert werden. Bei diesen ist der Zusammenhang zu Aufgaben „mit 10“ herzustellen. Auch hier wird der Zusammenhang sowohl durch die Lehrkräfte als auch die Lernenden dargestellt sowie versprachlicht (vgl. Gaidoschik, 2015), z.B.:

Gerade Kindern mit Schwierigkeiten Zusammenhänge und Beziehungen immer wieder in den Blick genommen werden, „damit deutlich wird, dass es sich um ein Aufgabenkriterium handelt und nicht darum, ob die Aufgabe individuell von einem Kind als einfach beziehungsweise leicht empfunden wird“ (Häsel-Weide et al., 2015, S. 138).

Mögliche Aufgabenstellungen

Diese Zusammenhänge können zunächst an der Tafel im Plenum gezeigt und besprochen werden. Anschließend sind Aufgaben in Partnerarbeit möglich. Beispielsweise können verschiedene Aufgaben danach sortiert werden, ob die Lernenden sie als „einfach“ oder „schwierig“ einstufen. Dazu können beispielsweise die Aufgabenkarten des Memory-Spiels aus dem Teilmodul „Grundlegendes Üben“ genutzt werden.

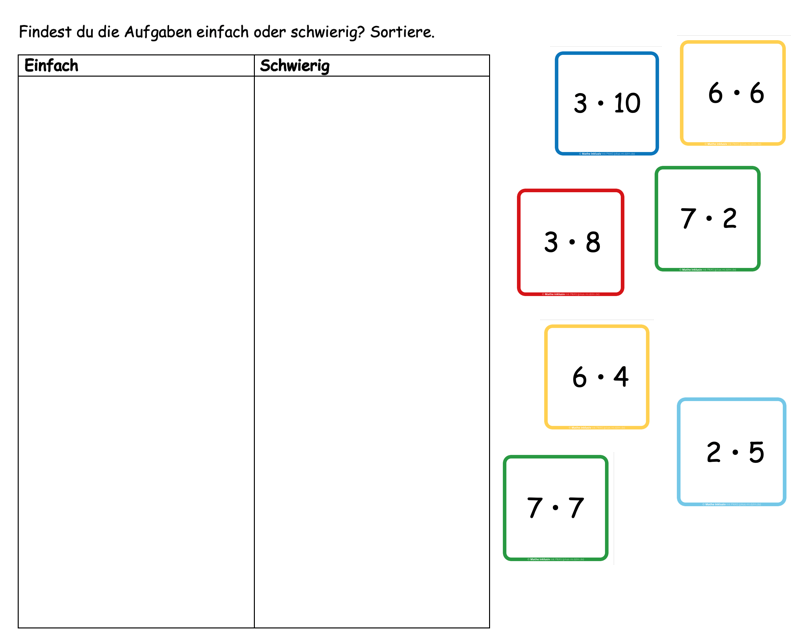
Die Sortierung soll jeweils begründet werden. Als Unterstützung können hier die zuvor benannten Kriterien und die Sprachvorbilder dienen. Eine mögliche Umsetzung ist, dass die Kinder zunächst alleine arbeiten und dann in Partnerarbeit ihre Einordnungen vergleichen und jeweils mündlich begründen, warum sie bestimmte Aufgaben als „einfach“ oder „schwierig“ bewerten. Anschließend sollen sie für zwei Aufgaben gemeinsam formulieren, warum diese Aufgaben einfach sind.

Eine mögliche Unterstützung, die Versprachlichung der Kriterien der Einfachheit zu begleiten, kann sein, den Kindern Satzbausteine zur Verfügung zu stellen. Dadurch kann auch der Schreibaufwand der Kinder reduziert werden.

Die Aufgabe ist einfach, weil...

• das Ergebnis das Doppelte von____________ist.
• das Ergebnis zehn mal so groß wie____________ist.
• das Ergebnis die Hälfte von____________ist.
• sie nahe an der Aufgabe____________ist.

 

Abschließend können in einer gemeinsamen Plenums-Phase die einfachen Aufgaben sowie die Begründungen gesammelt und reflektiert werden. An dieser Stelle kann auch das Gespräch auf Tauschaufgaben kommen. Diese sollte immer mitgedacht werden, da dann aus zunächst schwierigen Aufgaben (wie z.B. 8 · 5) eine einfache Aufgabe (wie z.B. 5 · 8) wird, die mit den bekannten Kriterien gelöst werden kann oder schon automatisiert ist.

Für leistungsschwache Kinder besteht bei dieser Aufgabe das Ziel darin, zu erkennen, dass es einfache Aufgaben gibt. Diese können mithilfe von Zusammenhängen und ohne zu zählen gelöst werden. Wenn Kinder diese Aufgaben noch nicht ‚einfach so‘ können, bietet es sich an, beispielsweise Übungskarten gezielt für die einfachen Aufgaben zu erstellen. Diese sollten immer wieder geübt werden, da sie zentral für die weiteren Ableitungsstrategien sind. Für diese Kinder kann es außerdem hilfreich sein, die Strategien einzeln zu thematisieren. Gerade wenn es Kinder gibt, die die Aufgaben „mit 5“ als (individuell) schwierig ansehen, ist dies von Bedeutung. Mögliche Umsetzungen können z.B. sein, sogenannte 5mal-Tage auszurufen, an denen gezielt die Zusammenhänge zwischen Aufgaben „mit 5“ und „mit 10“ betrachtet werden. Das Ziel ist es dabei, dass die Kinder z.B. beginnend mit Steckwürfelstangen eigene Wege zur Lösung der Aufgaben finden, diese an verschiedenen Beispielen erproben und schließlich absichern können (vgl. Gaidoschik, 2015). Für leistungsstärkere Kinder besteht das Ziel der Aufgabe darin, die Kriterien der Einfachheit zu beschreiben und auf neue Aufgaben zu übertragen (vgl. Häsel-Weide et al., 2015). Dabei ist wichtig, dass die Kinder die einfachen Aufgaben kontinuierlich üben und immer wieder die Strategien den Aufgaben zuordnen.

Verwandte Aufgaben erkennen und Zusammenhänge beschreiben

Um schwierige Aufgaben mithilfe von einfachen Aufgaben lösen zu können, ist ein zentrales Ziel, verwandte Aufgaben zu erkennen und diese Verwandtschaft beim Lösen zu nutzen. Solche Aufgaben werden auch Hilfsaufgaben genannt. Dabei sollen die Lernenden zunächst die Auswirkung der Veränderung eines Faktors auf das Ergebnis erkennen. Diese Veränderung wirkt sich anders aus als die Kinder es von der Addition oder Subtraktion gewohnt sind: Bei einer Änderung eines Faktors um 1 verändert sich das Ergebnis in der Regel nicht um 1, sondern um die Größe des anderen Faktors (vgl. Wittmann/Müller, 2017). Ändert sich der 1. Faktor um 1, wie beispielsweise von 5 · 7 zu 6 · 7, kommt am Punktebild eine (horizontale) Reihe von 7 Punkten dazu.

Soll beispielsweise die Aufgabe 8·9 gelöst werden, könnte die Tauschaufgabe genutzt werden, also 9 · 8. Dann ist die Hilfsaufgabe 10 · 8, und es wird eine Achterreihe weggenommen.
Wird allerdings 8 · 10 als Hilfsaufgabe genutzt, ändert sich der 2. Faktor, wodurch sich die Veränderung durch die unterschiedliche Bedeutung der Faktoren am Punktebild anders auswirkt: Es wird in jeder (vertikalen) Reihe ein Punkt weggenommen, also insgesamt 8 Punkte.

Bei einigen Hilfsaufgaben ändert sich der Faktor nicht um 1, sondern um 2. Auch diese Zusammenhänge müssen verdeutlicht werden, wie beispielsweise der Zusammenhang zwischen 5 · 8 und 7 · 8:

Damit Kinder über diese Zusammenhänge zwischen den Aufgaben nachdenken, müssen sie diese erkennen und beschreiben. Dabei liegt nicht mehr nur die Darstellung der Operation im Fokus der Aufmerksamkeit, sondern vor allem die Veränderung der Operation, um eine Hilfsaufgabe nutzen zu können. Der Schwerpunkt verlagert sich zunehmend von der Darstellung auf die Vorstellung, die Frage „Was genau wird verändert und warum?“ thematisiert diese Zusammenhänge zwischen verwandten Aufgaben (vgl. Häsel-Weide et al., 2015). Gerade für Kinder mit Rechenschwierigkeiten ist es wichtig, dass diese Zusammenhänge explizit gemacht werden, damit alle Schülerinnen und Schüler Ableitungsstrategien flexibel nutzen können.

Mögliche Aufgaben

Zunächst sollen die Kinder Veränderungen ausgehend von einfachen Aufgaben in den Blick nehmen und beschreiben. Dazu werden einfache Aufgaben systematisch verändert, wodurch der Blick der Kinder „explizit auf die Beziehungen zwischen Aufgaben und Darstellungen unterschiedlicher Aufgaben am Punktefeld gerichtet“ (Häsel-Weide et al., 2015, S. 142) wird.

Eine mögliche Umsetzung ist, dass die Kinder einfache Aufgaben und mögliche Veränderungen zufällig einander zuordnen und dann jeweils die einfache Aufgabe sowie die neu entstandene Aufgabe mit Ergebnis notieren. Hier können erneut die Aufgabenkarten aus dem Teilmodul „Grundlegendes Üben“ genutzt werden, die mit den folgenden Sätzen kombiniert werden können:

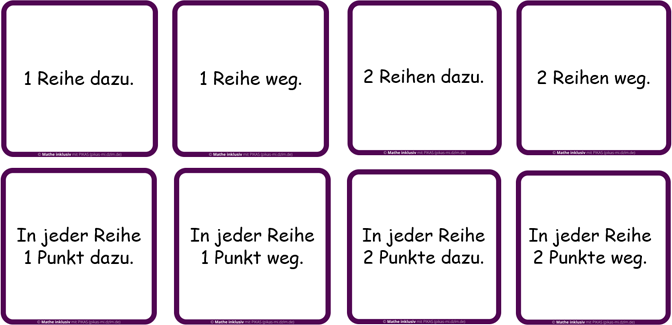
Durch die verschiedenen Kombinationsmöglichkeiten entstehen vielfache Beziehungen. Je nach Kind können die Aufgaben in symbolischer oder bildlicher Form zur Verfügung gestellt werden. Die beiden entstehenden Aufgaben werden im Heft notiert. Mögliche Kombinationen mit Beschreibung sind hier abgebildet:

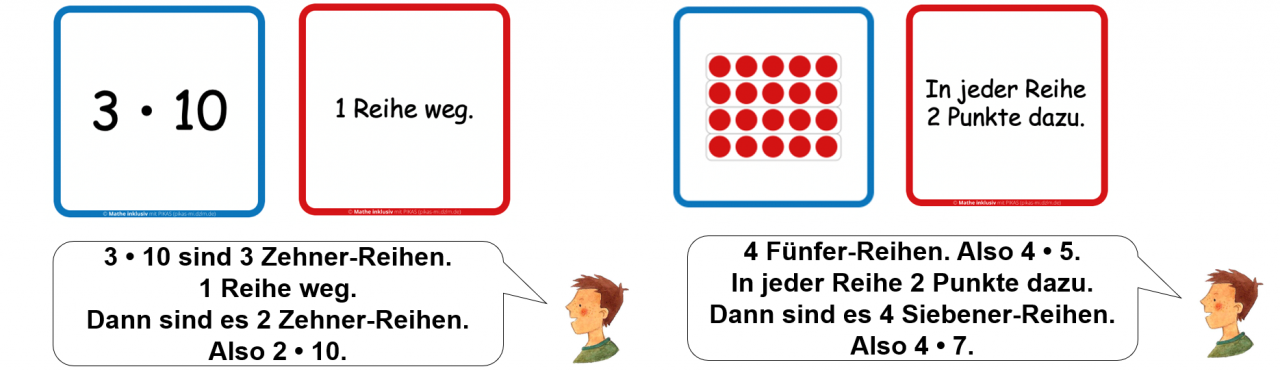
Für Kinder mit Schwierigkeiten kann die Anzahl der Aufgaben sowie der Zahlenraum verringert werden. Außerdem kann es hilfreich sein, nicht alle Kriterien auf einmal zur Verfügung zu stellen.

Zentral bei dieser Aufgabe ist nicht, dass Ableitungsaufgaben entstehen müssen, sondern dass strukturelle Zusammenhänge beschrieben werden.

Eine weitere Möglichkeit, das Erkennen von Zusammenhängen zwischen Aufgaben zu üben, besteht darin, dass die Kinder bei Aufgabenserien zunächst die für sie einfachste Aufgabe ankreuzen und diese berechnen. Anhand dieser sollen dann die weiteren Aufgaben berechnet werden.

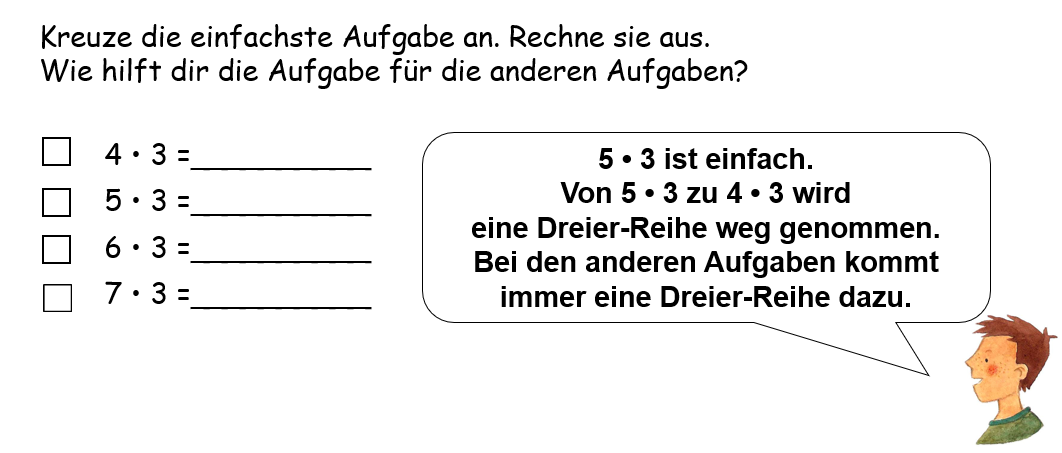
So wird nochmals verdeutlicht, dass Rechenaufwand gespart wird, wenn Beziehungen zwischen Aufgaben genutzt werden. Dabei steht sowohl im Mittelpunkt, die einfache Aufgabe zu identifizieren als auch das Nutzen der Verwandtschaft der Aufgaben, sodass die Aufgaben nicht isoliert betrachtet werden (vgl. Häsel-Weide et al., 2015). Die Kinder sollen dabei lernen, wie sich die Variation eines Faktors auf das Ergebnis auswirkt (vgl. Wittmann/Müller, 2017). Auch hier kann ein zusätzlicher Auftrag sein, die Aufgabe zusätzlich am Punktebild darzustellen:

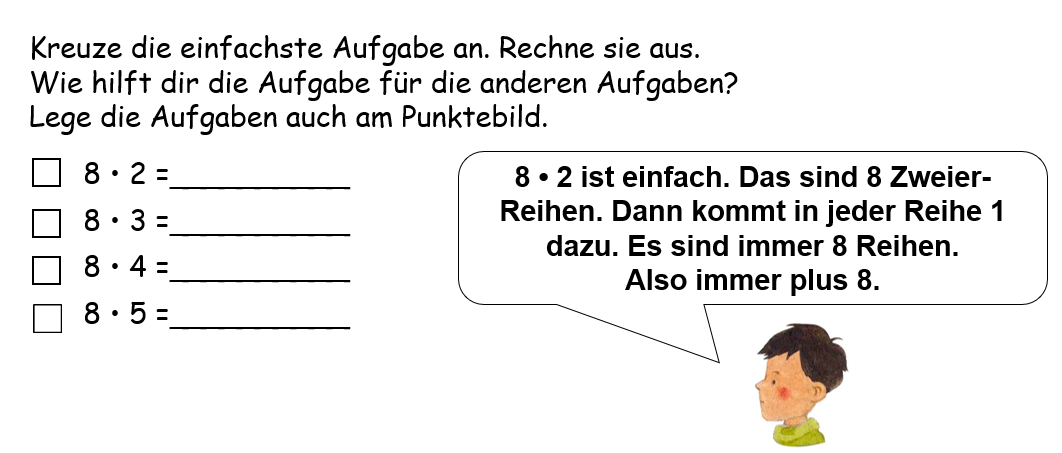
Mit dieser Aufgabe sollen die vorher erarbeiteten Zusammenhänge erneut in den Blick genommen werden, weshalb auch die Veränderungen in den operativen Aufgabenserien vielfältig sein müssen.

Eine Variante der Aufgabe ist, dass die Kinder zu vorgegebenen einfachen Aufgaben selbst verwandte Aufgaben finden und den Zusammenhang beschreiben. So haben sie auch die Möglichkeit, andere als die bisher erarbeiteten Beziehungen einzubringen (vgl. Häsel-Weide et al., 2015).

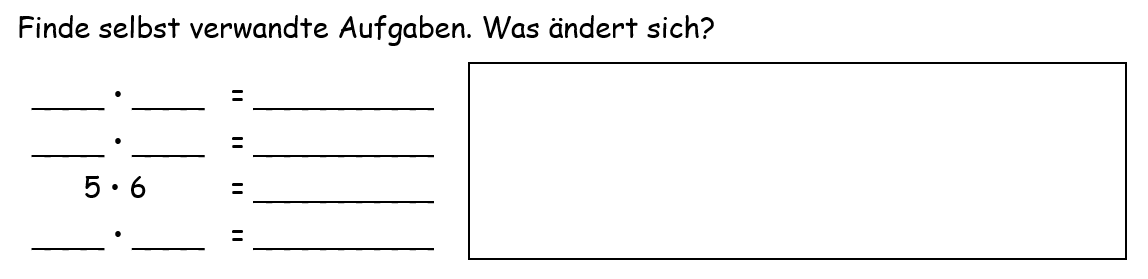
Hier kann zusätzlich der Hinweis gegeben werden: „Wenn du keine Idee hast, wie kannst du den Malwinkel verschieben? Welche Aufgaben entstehen? Was verändert sich?“, sodass auch an dieser Stelle der Bezug zum Punktefeld hergestellt werden kann.

Für Kinder mit Schwierigkeiten können Aufgaben mit kleineren Zahlenwerten gewählt werden, sodass Zusammenhänge in den Blick genommen werden können.

Im Austausch über die Aufgaben (im Plenum oder Partnerarbeit) steht das Erkennen und Beschreiben der Aufgabenbeziehungen im Mittelpunkt.

Um die Kinder anzuregen zu überlegen, für welche Aufgaben die Kernaufgaben helfen können, gibt es verschiedene Möglichkeiten. Beispielsweise können sie gemeinsam überlegen, welche verwandten Aufgaben sie zu einer Kernaufgabe finden und diese jeweils sammeln und vergleichen (vgl. Häsel-Weide et al., 2015). Eine andere Möglichkeit ist, dass sie die einfachen Aufgaben auf Karteikärtchen schreiben und auf der Rückseite aufschreiben, für welche Aufgaben diese Aufgabe helfen kann. Diese können dann in Partnerarbeit oder im Plenum verglichen werden, sodass auch deutlich wird, dass es nicht immer nur einen Weg gibt, abzuleiten (vgl. Gaidoschik, 2015).

Hier bietet sich eine Reflexion im Plenum an, bei der gesammelt wird, welche unterschiedlichen Aufgaben die Kinder gefunden haben. Zentral ist an dieser Stelle, dass die Kinder beschreiben, wie die einfache Aufgabe für die schwierige Aufgabe hilft, also die Verwandtschaft der Aufgaben explizit gemacht wird.

Verwandtschaft beim Lösen von schwierigen Aufgaben nutzen

Nachdem verschiedene Beziehungen thematisiert und einfache Aufgaben in den Zusammenhang zu schwierigen Aufgaben gesetzt wurden, steht nun im Vordergrund, das Ergebnis der schwierigen Aufgabe aus dem bereits ermittelten Ergebnis abzuleiten (vgl. Häsel-Weide et al., 2015). Das Ziel beim vernetzenden Üben ist, dass möglichst alle Kinder selbständig einfache Aufgaben nutzen können, um schwierige zu lösen. Oft gelingt es Kindern mit Rechenschwierigkeiten zwar, die Verwandtschaft von Aufgaben zu erkennen, die selbstständige Anwendung bereitet ihnen jedoch Schwierigkeiten (vgl. Gaidoschik, 2015). Deshalb ist es wichtig, dass verschiedene Strategien im Unterricht thematisiert werden und auch die Nutzung von Tauschaufgaben in den Blick genommen wird (vgl. Gaidoschik, 2015).

Mögliche Strategien sind hierbei:

• Aufgaben „mit 2“ helfen bei Aufgaben „mit 3“
• Aufgaben „mit 5“ helfen bei Aufgaben „mit 4“ und „mit 6“
• Aufgaben „mit 10“ helfen bei Aufgaben „mit 9“
• Quadrataufgaben helfen bei Nachbaraufgaben

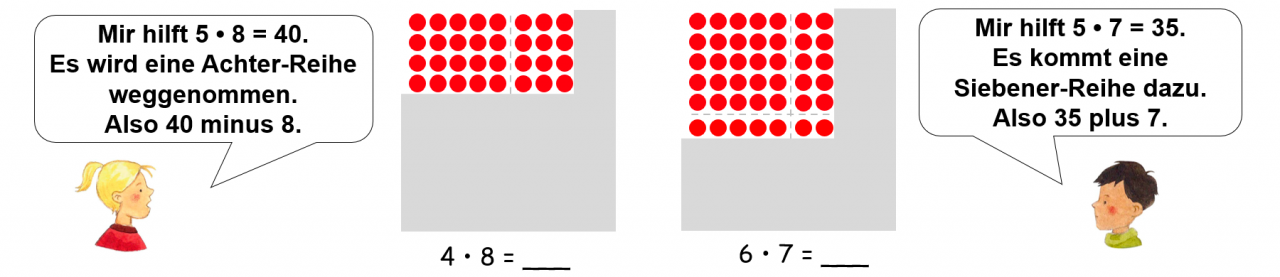
Auch zu den Aufgaben „mit 7“ und „mit 8“ lassen sich Ableitungsstrategien finden, z.B. können Aufgaben „mit 5“ helfen, zu der dann „… mal 2‘“oder „… mal 3“ dazugerechnet wird oder es werden verwandte Quadrataufgaben zum Lösen genutzt. Wichtig ist, dass die Kinder die Möglichkeit bekommen, selbst für sie passende Strategien zu entwickeln und diese darstellen sowie versprachlichen:

Darüber hinaus hilft es häufig auch, den Fokus der Kinder auf die Tauschaufgaben zu legen. Einige Kinder sehen die Aufgaben isoliert und betrachten deren Tauschaufgaben nicht. Deshalb sollten auch immer die Tauschaufgaben mit thematisiert werden, z.B.: „Prüf erstmal die Tauschaufgabe, vielleicht kannst du die ja schon“ oder „Nutze die Tauschaufgabe. Vielleicht kannst du dann eine Hilfsaufgabe finden“.

Für einige Kinder kann es hilfreich sein, dass die Strategien einzeln thematisiert werden und diese dann auch über einen längeren Zeitraum hinweg im Zentrum stehen (vgl. Gaidoschik, 2015). Die erarbeiteten Strategien bilden dann die Basis für das entdeckende und sichernde Üben.

Mögliche Aufgaben

Eine Möglichkeit, die Strategien zu üben, bietet die folgende Aufgabe, bei der die Kinder gezielt eine Strategie nutzen sollen:

So können verschiedene der oben angesprochenen Strategien geübt werden, indem die Lernenden zu jeder Strategie verschiedene Aufgaben berechnen und den Zusammenhang beschreiben. Eine Erweiterungsmöglichkeit ist hier, den Lernenden Aufgaben unterschiedlicher Strategien zur Verfügung zu stellen.

Fällt es den Lernenden schwer, den Zusammenhang zwischen der einfachen und schwierigen Aufgabe zu erkennen, können entsprechende Impulse gegeben werden: „Was ändert sich? Was kommt dazu? Wie viele Punkte sind es jetzt insgesamt?“. Zudem kann für leistungsschwächere Lernende der Zahlenraum angepasst werden, indem zunächst die Strategien im Raum bis 5 · 5 thematisiert werden. Zentral ist, dass die Kinder die Zusammenhänge zwischen den Aufgaben erkennen und diese zum Lösen der schwierigeren Aufgabe nutzen.

Um zu üben, selbständig schwierige Aufgaben mithilfe von einfachen Aufgaben zu lösen, können Aufgabenkarten erstellt werden, bei denen die Kinder selbst auswählen, welche einfache Aufgabe ihnen hilft, die schwierige Aufgabe zu lösen. Der Zusammenhang soll jeweils im Punktebild dargestellt und beschrieben werden. Diese Karten können dann auch für das Sichernde Üben genutzt werden.

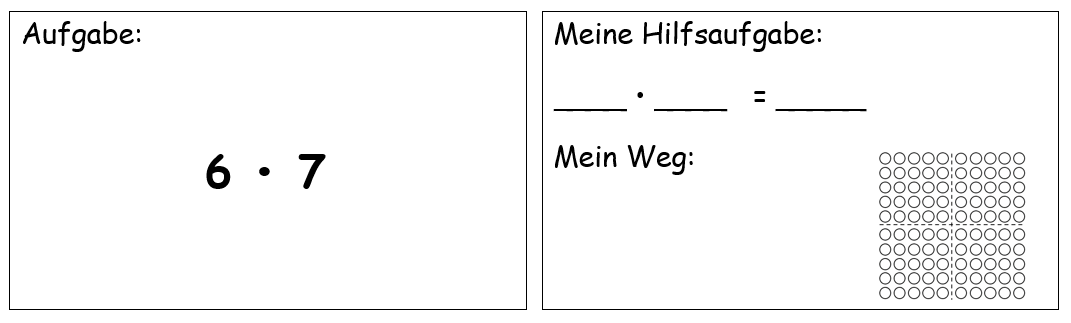
Finden die Kinder keine verwandten einfachen Aufgaben, können Impulse gegeben werden wie z.B.: „Wenn du auf dem Punktebild eine oder zwei Reihe(n) dazu/weg nimmst, kannst du dann eine einfache Aufgabe erreichen? Wie rechnest du dann weiter?“

Eine weitere mögliche Umsetzung besteht darin, dass die Kinder selbständig zu bestimmten Aufgaben Hilfsaufgaben finden. Anschließend wird im Plenum verglichen, welche Hilfsaufgaben die Kinder jeweils gewählt haben, sodass deutlich wird, dass es mehrere Möglichkeiten gibt, die schwierigen Aufgaben zu lösen.