Im Unterrichtsteil soll nun beispielhaft erläutert werden, wie die unterschiedlichen Vorerfahrungen zum Inhalt „Operationsvorstellungen Multiplikation“ berücksichtigt werden können, um individuelle Prozesse des Weiterlernens zu unterstützen.
Grundlage bildet die schon im Einstieg genannte Standortbestimmung Multiplikation verstehen des Partnerprojektes Mathe sicher können. Abgefragt wird dabei die Kompetenz, multiplikative Strukturen in verschiedenen Darstellungen zu deuten und selbst darzustellen. Sie wurden zum Schuljahresbeginn in einer inklusiven 5. Klasse einer Hauptschule durchgeführt, um zu überprüfen, welches Verständnis der Multiplikation die Kinder aus der Grundschule mitbringen. Die Standortbestimmung wurde von insgesamt 18 Schülerinnen und Schülern bearbeitet.
Schauen Sie sich die Aufgaben und die verschiedenen Schülerlösungen an. Welche Erklärungen finden Sie und wie könnte eine Förderung aussehen?
Lösungen der Lernenden und Förderhinweise
Multiplikation verstehen – Gruppierungen
Bei dieser Aufgabe geht es darum, gruppierte Darstellungen zu interpretieren, in einen Term zu übersetzen und auf Grundlage eines Terms selbst zu bilden. Gruppierte Darstellungen sind deshalb von Bedeutung, weil mit ihnen das grundlegende Verständnis der Multiplikation als Zusammenfassung gleichmächtiger Gruppen erarbeitet werden kann. Gleichzeitig stellt die Interpretation dieser Darstellung als Multiplikation für einige Lernende eine besondere Schwierigkeit dar, weil nicht beide Faktoren als Objekte erkennbar sind, da der Multiplikator nur als Anzahl der Gruppen vorliegt.
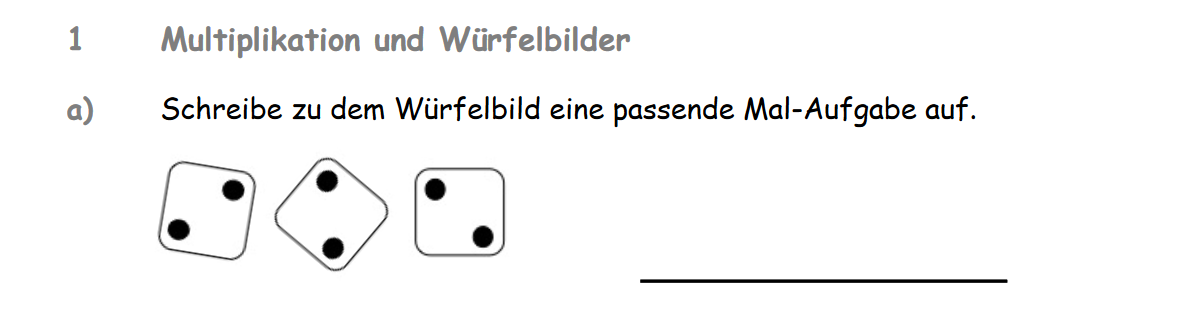 Aufgabe 1a) Multiplikation und Würfelbilder
Aufgabe 1a) Multiplikation und Würfelbilder
 Schülerlösungen (Auswahl)
Schülerlösungen (Auswahl)
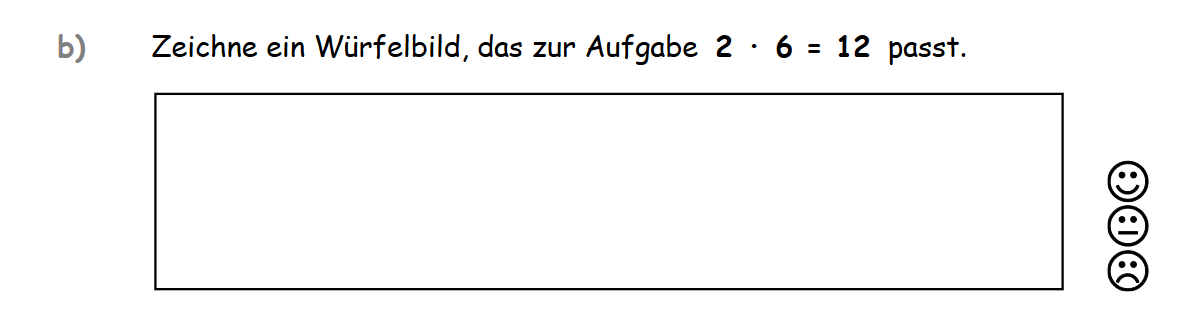 Aufgabe 1b) Multiplikation und Würfelbilder
Aufgabe 1b) Multiplikation und Würfelbilder
 Schülerlösungen (Auswahl)
Schülerlösungen (Auswahl)
Multiplikation verstehen – Flächen
Hier geht es darum, die flächige Darstellung einer Schokoladentafel als Multiplikation zu interpretieren und in einen Term zu übersetzen. Flächige Darstellungen gehören zu den wichtigsten Darstellungen der Multiplikation, insbesondere durch ihre Nutzungsmöglichkeit für die Veranschaulichung von Rechengesetzen und für multiplikative Strukturen in anderen Zahlbereichen.
 Aufgabe 2 - Multiplikationen in der Umwelt
Aufgabe 2 - Multiplikationen in der Umwelt
 Schülerlösungen (Auswahl)
Schülerlösungen (Auswahl)
Multiplikation verstehen – Punktebilder
In dieser Aufgabe werden mehrere Darstellungen kombiniert – zusätzlich zu den zwei korrekt als Multiplikation interpretierbaren Darstellungen des Punktefeldes und der gruppierten Darstellung gibt es auch zwei Darstellungen, die keine Multiplikationsaufgabe repräsentieren.
 Aufgabe 3 - Multiplikation und Punktebilder
Aufgabe 3 - Multiplikation und Punktebilder
 Schülerlösungen (Auswahl)
Schülerlösungen (Auswahl)
Multiplikation verstehen – Rechengeschichten
Mit Rechengeschichten können einfache Umweltbezüge hergestellt werden, die die Multiplikation für verschiedene Sachsituationen anwendbar machen. Falls die Kinder das Aufgabenformat „Rechengeschichte“ nicht kennen, ist hier ein Beispiel vorangestellt. Die Aufgabe besteht nun darin, zu einem Term selbst eine Sachsituation zu erfinden.
 Aufgabe 4 - Multiplikation und Rechengeschichten
Aufgabe 4 - Multiplikation und Rechengeschichten
 Schülerlösungen (Auswahl)
Schülerlösungen (Auswahl)
Multiplikation verstehen – Sprünge auf dem Zahlenstrahl
Die Multiplikation lässt sich auch anhand gleich großer Sprünge am Zahlenstrahl darstellen, diese Vorstellung ist beispielsweise auch bei der Multiplikation von Dezimalzahlen von Bedeutung und kann dort wieder aufgegriffen werden. Für einige Lernende kann die Interpretation des Zahlenstrahls jedoch eine eigene Hürde darstellen.
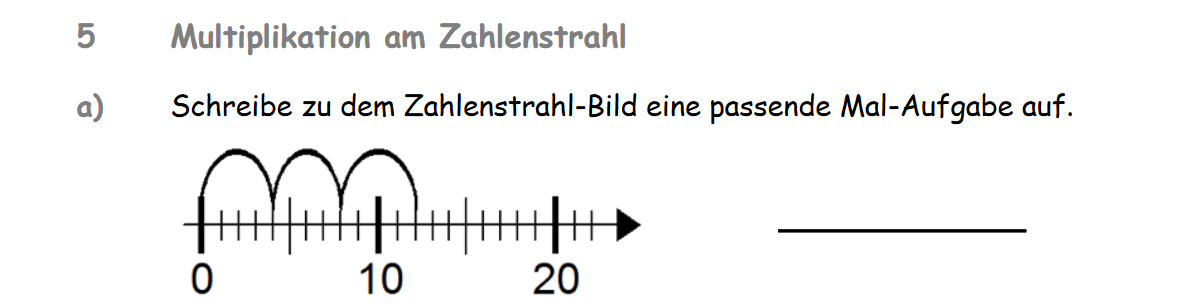 Aufgabe 5a - Multiplikation am Zahlenstrahl
Aufgabe 5a - Multiplikation am Zahlenstrahl
 Schülerlösungen (Auswahl)
Schülerlösungen (Auswahl)
Häufige Fehler
Einzelne Elemente werden übersetzt
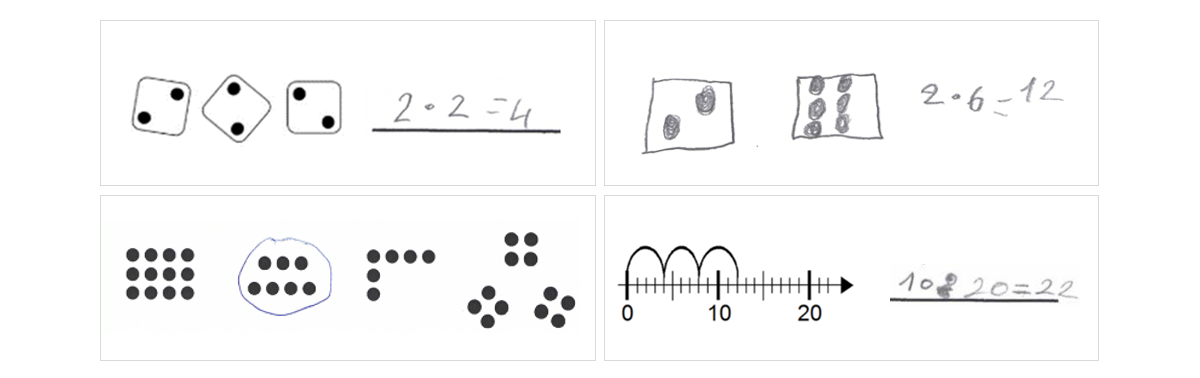 Abbildung 1 - Einzelne Elemente werden übersetzt
Abbildung 1 - Einzelne Elemente werden übersetzt
Eine fehlerhafte Strategie, die besonders häufig und bei einzelnen Lernenden über mehrere Aufgabentypen hinweg beobachtet werden konnte, ist das Übersetzen einzelner Elemente von einer Darstellungsweise in die andere, ohne die multiplikative Struktur zu berücksichtigen. Die Lernenden versuchen dabei einzelne Zahlen, die sie im Term oder der Darstellung sehen, in der anderen Darstellung wiederzufinden oder selbst zu produzieren. Eine grundsätzliche Vorstellung der Multiplikation schien entweder nicht vorhanden zu sein – oder die Lernenden aktivierten (analog zum Phänomen der „Kapitänsaufgaben“) keine Vorstellungen, die über den Zahlaspekt hinaus gehen. In jedem Fall scheint hier weitere Diagnose und eine grundlegende Förderung der Operationsvorstellungen zur Multiplikation notwendig.
Unterschiedliche Interpretation der Faktoren in Multiplikator und Multiplikand
In vielen Schülerlösungen zeigt sich, dass diese zwar die unterschiedliche Bedeutung der Faktoren verstanden haben, in der Interpretation von verschiedenen Darstellungen (z.B. Punktefeld oder Term) aber nicht konsequent jeweils einem Faktor eine bestimmte Rolle zukommen lassen.
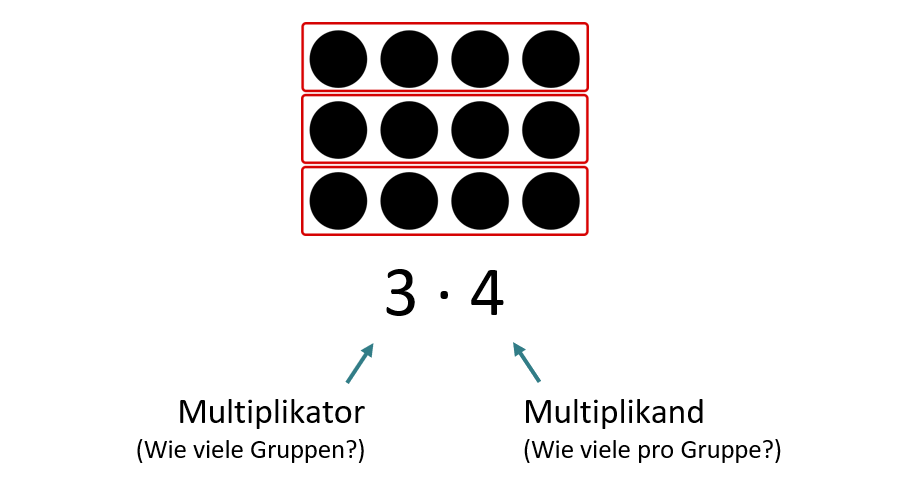 Abbildung 2 - Unterscheidung von Multiplikator und Multiplikand
Abbildung 2 - Unterscheidung von Multiplikator und Multiplikand
Für eine tragfähige Vorstellung der Multiplikation sollten die Lernenden zwischen den Rollen der Faktoren unterscheiden und diese auch sprachlich ausdrücken können. Diese Unterscheidung kann durch bewusste Sprache und Begründungen unterstützt werden („Wo siehst du drei Vierer?“).
 Abbildung 3 - Operationsverständnis Multiplikation auf PIKAS kompakt - Die Unterscheidung der Faktoren in Multiplikator und Multiplikand ist nicht in allen Darstellungen eindeutig, zum Teil beruht die Zuordnung auf Konventionen.
Abbildung 3 - Operationsverständnis Multiplikation auf PIKAS kompakt - Die Unterscheidung der Faktoren in Multiplikator und Multiplikand ist nicht in allen Darstellungen eindeutig, zum Teil beruht die Zuordnung auf Konventionen.
In Deutschland gilt meist die erste Zahl als Multiplikator (Anzahl der Mengen) und die zweite Zahl als Multiplikand (Größe der Mengen). Bei der hier genannten Unterscheidung handelt es sich um eine in Deutschland festgelegte Konvention (Ruwisch 2002), die mathematisch jedoch nicht festgelegt ist. Somit sind andere Lösungen mit Begründungen der Kinder nicht falsch (z.B. 4 • 3 im Punktebild in Abbildung 3).
Fehler bei der linearen Darstellung der Multiplikation
Die Aufgabenstellungen „Sprünge am Zahlenstrahl“ haben die Mehrzahl der Lernenden nicht korrekt gelöst. Eine mögliche Begründung dafür kann sein, dass diese Darstellung der Multiplikation im Unterricht meist seltener genutzt wird als gruppierte oder flächige Darstellungen. Es kann aber auch darin begründet sein, dass zwar eine lineare Vorstellung der Multiplikation vorhanden ist, jedoch Schwierigkeiten im Umgang mit dem Zahlenstrahl haben. Inwiefern eine lineare Vorstellung der Multiplikation vorhanden ist, könnte mit einer Standortbestimmung oder auch mit einer einfacheren Darstellung, bspw. einer Reihe verschiedenfarbiger Plättchen überprüft werden.
 Abbildung 4 - Lineare Darstellung der Multiplikation als Plättchen-Reihe.
Abbildung 4 - Lineare Darstellung der Multiplikation als Plättchen-Reihe.
Ausführliche Informationen zur linearen Vorstellung der Multiplikation finden Sie bei PIKAS Kompakt unter der Rubrik „Operationsvorstellungen Multiplikation“.
Unterrichtsorganisation
Um sowohl Diagnose als auch Förderung sinnvoll und effizient im Klassenkontext durführen zu können, sind mehrere organisatorische Überlegungen notwendig.
Im Teilmodul Unterrichtsorganisation auf dieser Seite werden Aspekte einer diagnose- und fördergünstigen Unterrichtsorganisation dargestellt, auf dessen Grundlage eine Vielzahl an Diagnose- und Fördermomenten im Klassenverband ermöglicht werden können.