Es kommt in allen Unterrichtsfächern vor, dass mit einer neuen Unterrichtseinheit begonnen wird, obwohl einige Schülerinnen und Schüler die Inhalte der vorherigen noch nicht wirklich verstanden haben. In einigen Unterrichtsfächern ist dies weniger problematisch – sie haben die Möglichkeit, immer wieder „neu einzusteigen“. Im Fach Mathematik ist das nicht so: Die Unterrichtsinhalte bauen systematisch aufeinander auf, einzelne Inhalte werden über die Klassenstufen hinweg immer wieder aufgegriffen und weiterentwickelt. Um in den höheren Jahrgängen weiterlernen zu können, ist es unerlässlich, den Stoff der früheren Jahrgänge verstanden zu haben.
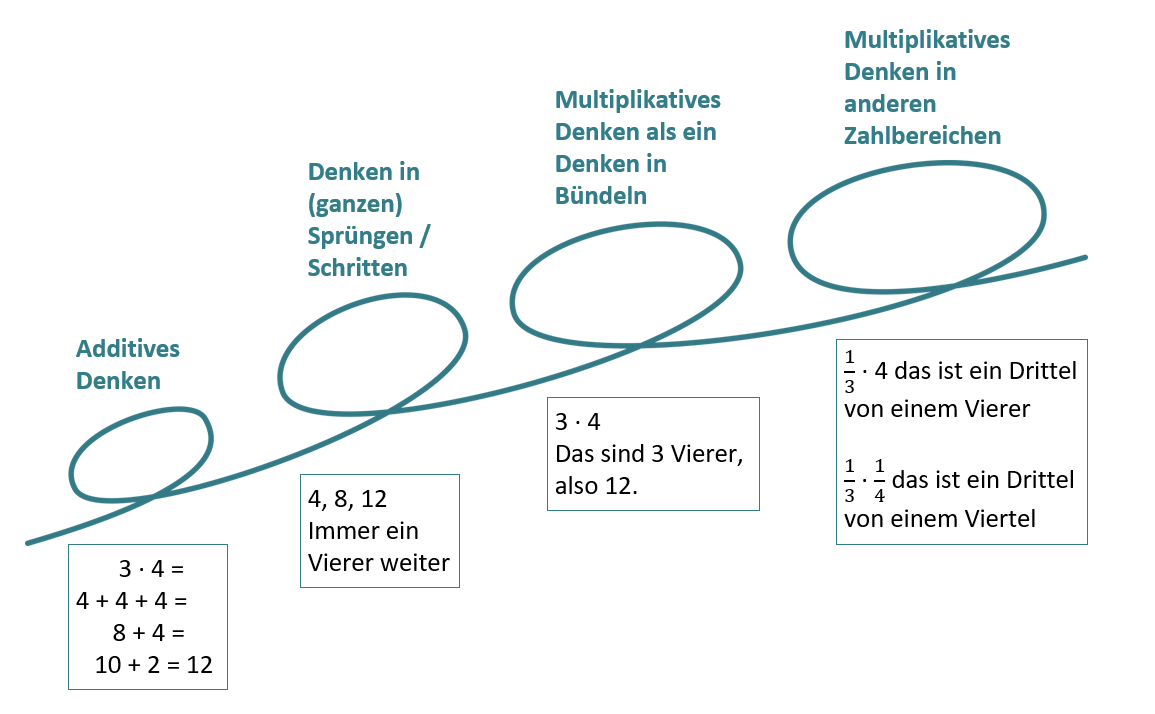 Abbildung 1 - Spiralprinzip Multiplikation: Einzelne Vorstellungen werden über die Klassenstufen hinweg immer wieder aufgegriffen und weiterentwickelt (in Anlehnung an Götze & Seidel, 2022, Folie 12; vgl. auch Götze & Baiker, 2021)
Abbildung 1 - Spiralprinzip Multiplikation: Einzelne Vorstellungen werden über die Klassenstufen hinweg immer wieder aufgegriffen und weiterentwickelt (in Anlehnung an Götze & Seidel, 2022, Folie 12; vgl. auch Götze & Baiker, 2021)
So wird beispielsweise in der Grundschule die Vorstellung der Multiplikation als fortgesetzte Addition weiterentwickelt zu einer Vorstellung, die Multiplikation als ein Denken in Bündeln versteht (vgl. Abbildung 1). Dies ist wiederum die Voraussetzung dafür, dass multiplikatives Denken in der Sekundarstufe auch in anderen Zahlbereichen, wie dem der Brüche, verständnisorientiert gelingen kann. Das multiplikative Verständnis als ein Denken in Bündeln ist für die weitere Lernentwicklung so bedeutsam, dass von einer unverzichtbaren Verstehensgrundlage gesprochen werden kann.
Als unverzichtbare Verstehensgrundlagen bezeichnen wir diejenigen inhaltlichen Vorstellungen und Darstellungen, die auch Lernende mit Schwierigkeiten beim Mathematiklernen in Klasse 5 beherrschen müssen, damit verständiges Weiterlernen in der Arithmetik der Sekundarstufe möglich ist.
(Prediger, Freesemann, Moser Opitz & Hußmann, 2013, S. 10)
Das Nicht-Beherrschen solcher Verstehensgrundlagen – hierzu zählen insbesondere ein tragfähiges Zahl-, Operations- und Stellenwertverständnis – kann als sicherer Prädiktor für Schwierigkeiten in Mathematik in der Klasse 8 gelten (Prediger, 2016, S. 366). Werden Lücken in den Verstehensgrundlagen nicht geschlossen, ist es wahrscheinlich, dass das Weiterlernen in der Sekundarstufe behindert wird und Lernfortschritte ausbleiben – auch dann, wenn der aktuelle Stoff mit großem Aufwand trainiert wird.
Diagnose und Förderung muss also grundsätzlich an fachdidaktisch-inhaltlichen Überlegungen ausgerichtet sein, die der kumulativen Struktur der Mathematik gerecht wird, wobei zwei zentrale Qualitätskriterien formuliert werden können (Häsel-Weide & Prediger, 2017, S. 4):
-
„Fachdidaktische Treffsicherheit: Welche Förderinhalte sind gemäß der fachdidaktisch-empirischen Forschung zentral, z.B. um mögliche Hürden zu überwinden?
-
Adaptivität: Wie gut ist die Förderung der zentralen Förderinhalte auf die individuellen Lernbedarfe der Einzelnen abgestimmt?“
Mögliche Planungsfragen für die Spezifizierung von Inhalten für die Diagnose und Förderung könnten dann wie folgt aussehen (vgl. ebd., S. 2):
Mit Blick auf die gesamte Klasse
-
Über welche inhalts- und prozessbezogenen Kompetenzen sollen welche Lernenden verfügen?
-
Welche inhaltlichen Vorstellungen sollen aufgebaut, welche Darstellungen eingeführt werden?
-
Welche Begriffe, Vorgehensweisen und Verfahren sollen die Lernenden erarbeiten?
-
Welche typischen Schwierigkeiten werden voraussichtlich auftauchen, die berücksichtigt werden müssen?
Mit Blick auf spezifische Potentiale der Lernenden
-
Welche anspruchsvollen kognitiven Aktivitäten können im selben Thema geplant werden?
-
Welche Möglichkeiten zur Vernetzung, Vertiefung und Erweiterung bieten sich?
-
Mit Blick auf spezifische Schwierigkeiten der Lernenden
-
Welche Verstehensgrundlagen sind für das Thema relevant?
-
Welches Lernangebot für zieldifferent unterrichtete Lernende ist thematisch passend?
Aus diesen Anforderungen ergeben sich für die Planung des Unterrichts verschiedene Konsequenzen.
Vorerfahrungen erheben
Um ein Lernangebot zu schaffen, das adaptiv an den individuellen Bedarfen der Lernenden orientiert ist, müssen die Vorerfahrungen der Lernenden erhoben werden. Nur wer ein realistisches Bild davon hat, was seine Schülerinnen und Schüler wissen und können, kann passende Lernangebote entwickeln und gezielt fördern (Häsel-Weide & Prediger, 2017, S. 1).
Zahlreiche Informationen dazu, wie individuelle Lernstände der Lernenden erhoben und Schlussfolgerungen für die Förderung gezogen werden können, finden Sie unter der Leitidee „Diagnosegeleitet fördern“. Dort liegt der Fokus häufig (aber nicht ausschließlich) auf der individuellen Diagnose und Förderung von einzelnen Lernenden, beispielsweise in Form von Diagnose- und Fördergesprächen.
Für die Durchführung im Klassenverband sind Standortbestimmungen (SOBen) geeignet. Diese enthalten meist eine Sammlung von Aufgabenstellungen zu einem Thema, die je nach Intention und gegebenen Möglichkeiten variieren können. Sie „dienen der fokussierten Ermittlung individueller Lernstände und finden an zentralen Punkten im Lehr-/Lernprozess statt – meistens zu Beginn oder zum Abschluss einer längeren Auseinandersetzung mit einem Rahmenthema“ (Sundermann & Selter, 2006, 21). Beim Einsatz ist entscheidend, dass den Kindern bewusst ist, dass es sich dabei nicht um Leistungskontrollen handelt, sondern das Erkenntnissinteresse der Lehrkraft im Vordergrund steht (Krauthausen, 2018, 245).
-
Vertiefende Informationen zum Einsatz von Standortbestimmungen finden Sie auf PIKAS.
-
Sammlungen von Standortbestimmungen zum jeweiligen Schuljahresbeginn, sowie zu unterschiedlichen mathematischen Inhalten, nach Zahlräumen sortiert, finden Sie im Bereich "Diagnose und Förderung" bei PIKAS.
-
Wenn Sie eigene Standortbestimmungen zu einem bestimmten Thema entwickeln möchten, finden Sie auf primakom Kriterien zur Erstellung von Standortbestimmungen und Beispielstandortbestimmungen zur Orientierung in neuen Zahlenräumen.
Treffsicher diagnostizieren
Ausgangspunkt aller diagnostischer Überlegungen sind stets inhaltliche Planungsfragen. Warum dies so wichtig ist, zeigt das folgende Beispiel: Zu Beginn der Sekundarstufe werden „traditionsgemäß die schriftlichen Rechenverfahren (wie schriftlich Multiplizieren) wiederholt“ (Prediger, 2016, S. 366). Zeigen sich hier bei einzelnen Lernenden Probleme, werden häufig nur die Rechenverfahren trainiert. Dies ist für die Kinder sinnvoll und effizient, die lediglich eine „Auffrischung“ der Regeln des schriftlichen Multiplizierens benötigen, weil ihnen der Rechenalgorithmus nicht mehr geläufig ist. „Viele Kinder, die sich die Regeln des schriftlichen Multiplizierens nicht stabil merken können, verfügen [aber] nicht über adäquate Verstehensgrundlagen zum Stellenwertsystem […] und zu Grundvorstellungen zu arithmetischen Operationen, insbesondere zur Bedeutung der Multiplikation und Division“ (ebd.). Diese Kinder werden dann zwar kurzfristig gefördert, aber es entsteht kein langfristiger Kompetenzaufbau.
Bei der Planung von Lernausgangslagendiagnosen sollte folglich immer auch geklärt werden, welche Verstehensgrundlagen für das aktuelle Thema relevant sein können. Dies ist besonders für Kinder mit Schwierigkeiten im Mathematiklernen bedeutsam, „da es ihnen oftmals schwerfällt, von sich aus mathematische Zusammenhänge zwischen Zahlen und Operationen zu sehen. Inhaltliche Vorstellungen und mathematische Beziehungen sind jedoch der bedeutungstragende Kern der Mathematik“ (Häsel-Weide & Prediger, 2017, S. 4f). Bei der Förderung sollte deshalb besonders darauf geachtet werden, „inwieweit die Lernenden belastbare inhaltliche Vorstellungen zu Zahlen, Operationen und dem Stellenwertsystem aufgebaut haben“ (ebd., S. 5).
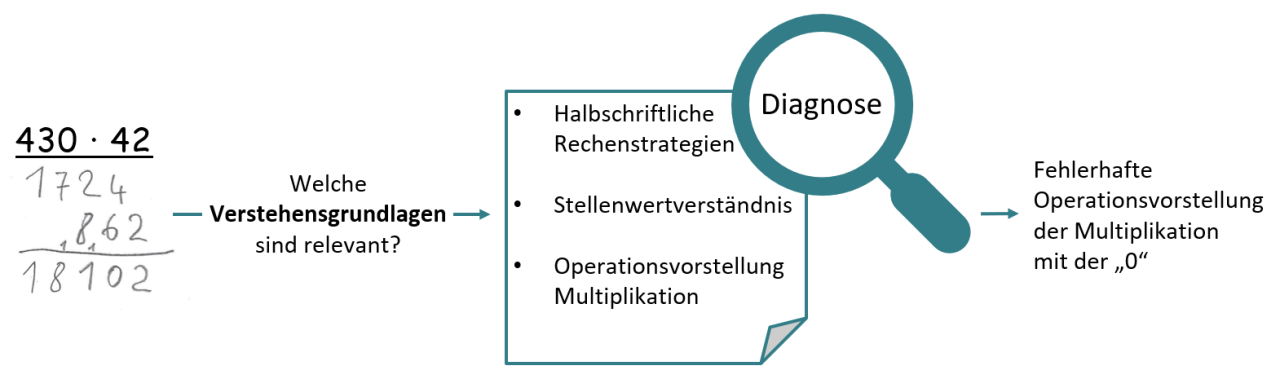 Abbildung 2 - Welche Verstehensgrundlagen sind für die schriftliche Multiplikation relevant?
Abbildung 2 - Welche Verstehensgrundlagen sind für die schriftliche Multiplikation relevant?
Zeigen sich also beispielsweise zu Beginn der Sekundarstufe bei der schriftlichen Multiplikation gehäuft Probleme, kann es notwendig sein, zunächst relevante Verstehensgrundlagen, wie halbschriftliche Rechenstrategien, das Stellenwertverständnis oder das Operationsverständnis zur Multiplikation in den Blick zu nehmen (vgl. Abbildung 2). Die Diagnose kann dabei mit weiteren Standortbestimmungen durchgeführt werden, häufig reichen aber auch kurze Diagnosegespräche oder Diagnoseaufgaben. Entscheidend ist, dass der Lehrkraft der Blick zurück, auf die Verstehensgrundlagen, gelingt.
In diesem Beispiel wird deutlich, dass das Problem nicht in einer fehlerhaften Ausführung des Algorithmus der schriftlichen Multiplikation liegt, sondern in einer fehlerhaften Operationsvorstellung der Multiplikation mit „0“.
Passgenau fördern
Wenn klar ist, an welcher Stelle Lücken in den Verstehensgrundlagen bestehen, kann die Förderung dort ansetzen und die Grundlage für anschlussfähiges Wissen schaffen. Das Ziel ist es, langfristig Kompetenzen aufzubauen, statt kurzfristig im aktuellen Unterrichtsstoff zu „reparieren“ (Prediger, Freesemann, Moser Opitz & Hußmann, 2013, S. 10). Dies geschieht vor allem dann, wenn sich Förderung am Aufbau von Verständnis orientiert.
Zusammenfassend lassen sich folgende zentrale Ideen als handlungsleitend für die Förderung bei Schwierigkeiten beim Mathematiklernen festhalten:
-
Schwerpunkt auf die Verstehensgrundlagen legen,
-
Aufbau von Vorstellungen in den Mittelpunkt stellen, statt Fertigkeiten und Lösungen, auch beim Vertiefen prozessbezogener Kompetenzen,
-
Veranschaulichungen und Materialien als Gegenstände zum Nachdenken nutzen, anstelle als Hilfsmittel zur reinen Ergebnisermittlung.
(Häsel-Weide & Prediger, 2017, S. 5)
Um dieser Verständnisorientierung gerecht zu werden, sollten Förderaufgaben bestimmte Eigenschaften besitzen. Hier folgt eine kurze Auswahl von Kriterien für Förderaufgaben, die die oben genannten zentralen Ideen konkretisieren. Ganz grundsätzlich ist von Bedeutung, dass die Förderaufgaben bei dem ansetzen, was die Kinder können, also kompetenzorientiert und diagnosegeleitet sind.
-
Handlungsorientierung berücksichtigen, indem z.B. in der Aufgabenstellung Materialarbeit integriert wird („Von der Handlung in den Kopf“) oder Material, das in der Diagnoseaufgabe nur bildlich dargestellt ist, konkret Verwendung findet. Hierbei sollten die Vorerfahrungen der Lernenden dahingehend berücksichtigt werden, dass entweder bekanntes Material genutzt wird oder neues Material eingeführt und erklärt wird.
-
Darstellungswechsel initiieren, indem z.B. verschiedene Darstellungen (enaktiv, ikonisch, symbolisch) zu den Förderaufgaben hinzugezogen werden. Auch hier sollte an die Vorerfahrungen der Lernenden angeknüpft werden, indem bekannte Darstellungen ausgewählt oder erweitert werden und über die Passung und Nicht-Passung von Darstellungen gesprochen wird.
-
zum Verbalisieren anregen, indem z.B. Beschreibungen, Erklärungen, Erläuterungen etc. von den Kindern eingefordert werden („Beschreibe deinen Rechenweg“, „Erkläre, warum/wie…“ usw.). Das Anlegen eines Wortspeichers ist an dieser Stelle von großer Bedeutung, da mit ihm sowohl die Vorerfahrungen der Lernenden zu einzelnen Begriffen und Formulierungen festgehalten als auch neue Begriffe für alle sichtbar dokumentiert werden können.
-
tiefergreifende Einsichten anbahnen, indem z.B. Aufgaben gestellt werden, die operative Veränderungen thematisieren („Was passiert, wenn…?“) oder Fragen ergänzt werden, die zum Reflektieren anregen („Warum ist das sinnvoll?“, „Warum macht man das so?“, „Was hilft dir, …?“). Dabei muss berücksichtigt werden, dass je nach Vorerfahrung das Beantworten solcher Fragen geübt werden muss.
Vertiefende Informationen zu Förderaufgaben finden Sie auf dieser Seite unter Diagnose- und Förderaufgaben.
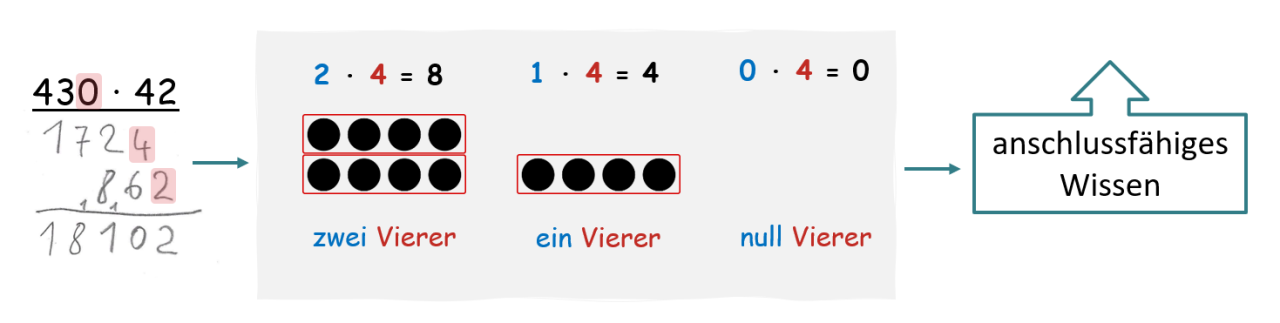 Abbildung 3 - Förderung von anschlussfähigem Wissen, mit dem Ziel eines langfristigen, verständnisorientierten Kompetenzaufbaus.
Abbildung 3 - Förderung von anschlussfähigem Wissen, mit dem Ziel eines langfristigen, verständnisorientierten Kompetenzaufbaus.
Beim Beispiel des fehlerhaften Operationsverständnis der Multiplikation mit der „0“ als Multiplikator (vgl. Abbildung 3) ist also von Bedeutung, dass die Förderung verständnisorientiert stattfindet und den Aufbau von Vorstellungen unterstützt, anstatt die Lösung vorzugeben und die Lernenden beispielsweise nur an die Regel „0 ∙ x = 0“ zu erinnern. Nur so kann ein langfristiger Kompetenzaufbau erfolgen. Als Förderaufgabe wären dann z. B. operative Serien in Verbindung mit Darstellungswechseln und der Anregung zum Verbalisieren von Veränderungen von Aufgabe zu Aufgabe möglich.