Schwierigkeiten bei der Simultanerfassung
Vereinzelt gibt es Kinder, die Schwierigkeiten bei der Simultanerfassung haben und selbst bei einer Darstellung von drei Elementen die Anzahl nur zählend ermitteln können.
Abbildung 2
Gaidoschik (2007) weist darauf hin, dass auch diese Kinder die Möglichkeit haben, Anzahlen strukturiert zu bestimmen, indem sie lernen, Darstellungen von Anzahlen am Zehnerfeld zu deuten, Strukturen hineinzusehen und die Darstellung von drei Elementen beispielsweise in ihrer Beziehung zur fünf (es fehlen noch zwei Elemente) zu erkennen.
Die Fähigkeit zur quasi-simultanen bzw. strukturierten Anzahlerfassung ist deshalb von so grundlegender Bedeutung, da erst durch sie der Aufbau geeigneter innerer Bilder und mentaler Vorstellungen der verschiedenen Anzahlen, d.h. der Aufbau tragfähiger Zahlvorstellungen und die Entwicklung von nicht-zählenden Rechenstrategien, gewährleistet wird. "Je besser ein Kind die gruppenweise Anzahlbestimmung beherrscht, desto leichter, schneller und sicherer kann es später rechnen“ (Wittmann & Müller, 2009, S. 15).
Das visuelle Unterteilen und strukturierte Erfassen größerer Mengen wird durch den Einsatz strukturierter Darstellungen sowie durch vorstrukturierte Materialien wie beispielsweise das 10er-, 20er- oder 100er-Punktefeld oder den Rechenrahmen, die den Bezug zu den Teilmengen 5 und 10 verdeutlichen, unterstützt (vgl. Schipper, 2008; Scherer & Moser Opitz, 2010).
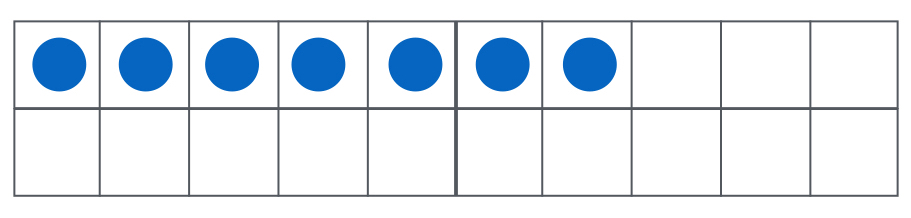Abbildung 3
Rechenschiffchen mit 20 Wendesteinen:
Abbildung 4
Abbildung 5
Abbildung 6
Mittels Übungen zum „schnellen Sehen“, bei denen den Kindern nur kurz – das Abzählen der Elemente wird so verhindert – strukturierte Mengenbilder gezeigt werden, kann die Fähigkeit des quasi-simultanen Erfassens und der Aufbau mentaler Bilder trainiert werden. Übungsideen und Beispiele zum "schnellen Sehen" finden Sie unter Unterricht: Schnelles Sehen.
Vor der Durchführung von Übungen zum "schnellen Sehen"
Bevor vorstrukturierte Arbeitsmittel – auch für Übungen zum "schnellen Sehen" – eingesetzt werden, sollten insbesondere Kinder mit Lernschwierigkeiten ausgiebig die Gelegenheit erhalten, mit verschiedensten Anordnungen von Elementen zu arbeiten, Zahlen darzustellen und Anzahlen zu bestimmen.
Wesentlich hierbei ist die Verknüpfung und Übersetzung zwischen und innerhalb der verschiedenen Repräsentationsformen wie Handlungen, Bilder, Symbole und Sprache.
D. h. es geht um das Wahrnehmen von Strukturen, um das Strukturieren und Anordnen von Elementen, das Hervorheben von Strukturen durch Handlungen und Markierungen oder das Bestimmen von Anzahlen. Anregungen, Ideen und Übungen hierzu finden Sie unter Unterricht: Muster legen.
Besonders wichtig ist es zudem, die Kinder immer wieder anzuregen, ihre Handlungen und die erfassten Zahldarstellungen, Zahlbeziehungen und Strukturen zu beschreiben und zu erläutern, verschiedene Darstellungen zu vergleichen und aufeinander zu beziehen (vgl. Kuhnke, 2013; Scherer & Moser Opitz, 2010; Söbbeke, 2003).
Es kann dabei durchaus sein, dass die vom Lehrer intendierte Struktur nicht gesehen wird und das Kind eine andere Deutung der Zahldarstellung vornimmt.
"Hier ist zu beachten, dass solche Zahldarstellungen nicht eine offensichtliche Struktur enthalten, sondern dass diese vom Individuum konstruiert bzw. hineingesehen werden muss und sich somit individuell unterscheiden [...] kann" (Scherer & Moser Opitz, 2010, S. 97).
Übungen zur strukturierten Anzahlerfassung – Kinder mit Lernschwierigkeiten
Insbesondere bei Kindern mit Lernschwierigkeiten ist wichtig, dass bei Übungen zur strukturierten Anzahlerfassung zunächst mit kleinen Anzahlen (< 10) gearbeitet wird. Den Kindern sollte genügend Zeit zur Anzahlermittlung (auch zählend!), zur Erkundung vorhandener Strukturen und zur Bildung eigener Strukturen beispielsweise durch Verschieben von Plättchen oder Markierungen und Zeichnungen gegeben werden. Besonders wichtig ist die sprachliche Begleitung der Handlungen und Aktivitäten (vgl. Scherer & Moser Opitz, 2010).
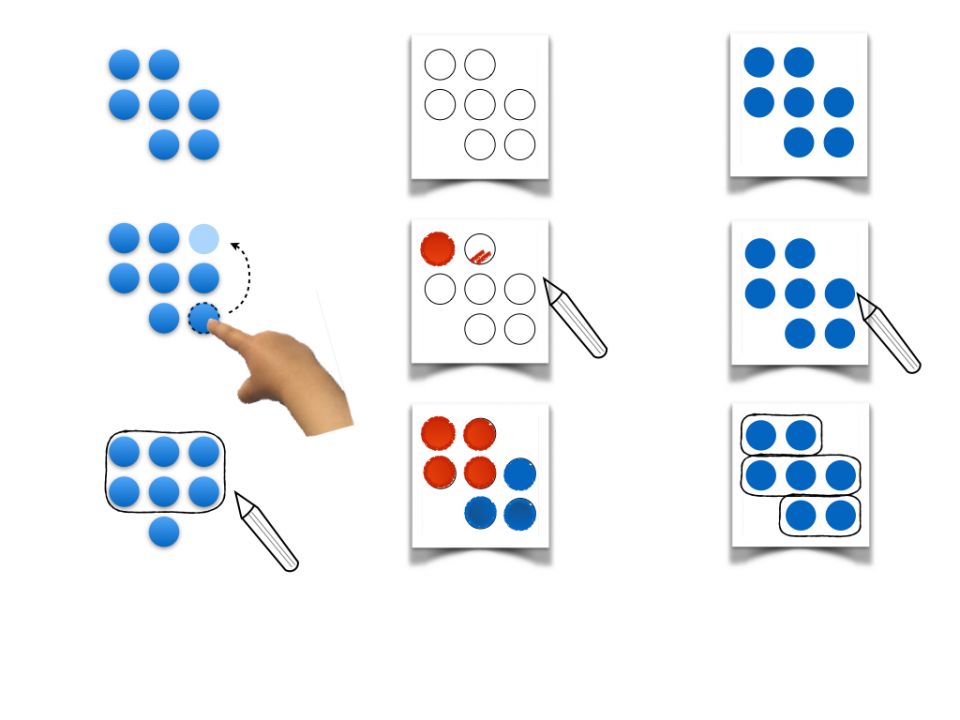Abbildung 7
Zahlen darstellen mit unstrukturierten und strukturierten Materialien
Bei den im Teilmodul Unterricht (s. Modul Zahlvorstellungen (ZR 0 bis 100)) dargestellten Unterrichtssequenzen und Aufgabenstellungen sowie den im Folgenden beschriebenen Beispielen für Unterrichtsaktivitäten, deren Schwerpunkt auf der Darstellung von Anzahlen liegt, handelt es sich zum einen um Aktivitäten mit unstrukturierten Materialien. Neben Aufgaben im Zahlenraum bis 20 geht es auch um Aufgabenstellungen mit Objekten der gleichen Art in größerer Anzahl.
Ein Beispiel für unstrukturierte Materialen, die sich gut für den Einsatz im Unterricht eignen und einen größeren Zahlenraum fokussieren sind sog. "Kapla-Steine".
Kapla-Steine bieten als Material einen besonderen Vorzug, da sie handlich von den Kindern auch bei feinmotorischen Schwierigkeiten sicher angeordnet werden können, auf der Grundlage ihrer unterschiedlichen Flächengrößen auch verschiedene Systematisierungen erlauben und zu guter Letzt Analogien zu einer Strichliste aufweisen, die im Sinne einer Abstrahierung aufgegriffen werden könnte.
Im Unterrichtsbeispiel zu den Kapla-Steinen (Unterricht: 100 darstellen) wird der Fokus genau auf solche Aktivitäten gelenkt, die es den Kindern ermöglichen, eigenständige Erkundungen der Bedeutung des Bündelns vorzunehmen: Sie sollen eine zunächst ungeordnet vorliegende Anzahl an Objekten über eigenständige Bündelungsprozesse so anordnen, dass die Menge überschaubar wird.
Abbildung 8
Der Aufbau dekadischer Einsichten fußt auf Gelegenheiten zur aktiven Auseinandersetzung mit konkreten Anzahlen, die letztlich eine dezimale Strukturierung erforderlich machen.
Dies gelingt gewiss nicht mit Zahlen bis 10 oder 20, schon eher aber mit Zahlen bis 100 oder darüber hinaus; also mit Anzahlen, die unüberschaubarer werden und zumindest eine Bündelung von 10 einzelnen Einern in 1 einzelnen Zehner, darauf aufbauend von 10 Zehnern in 1 Hunderter erforderlich machen. Denn es ist für die meisten Kinder im Anfangsunterricht nicht nur unökonomisch, sondern schlicht und einfach auch unmöglich bis 100 zu zählen. Daher wird es notwendig werden, kleinere Bündel zu zählen und mit den Bündeln weiter zu arbeiten.
Der zweite Schwerpunkt der Aufgabenbeispiele zur Darstellung von Zahlen liegt in Aktivitäten mit bereits vorstrukturierten didaktischen Materialien wie etwa dem 10er-, 20er- oder 100er-Punktefeld. Eine Idee für die Umsetzung im Unterricht finden Sie unter Unterricht: Muster im 10er Feld.
Bevor jedoch im Unterricht mit Punktefeldern gearbeitet wird, sollten die Kinder zunächst die Gelegenheit erhalten, über die Darstellung von Zahlen mit ihren Fingern Erfahrungen im Zahlenraum bis 10 zu sammeln. Die Finger „bieten durch ihre Struktur (zehn Finger verteilt auf zwei Hände zu jeweils fünf) beste Voraussetzungen dafür, um mit ihrer Hilfe zu wichtigen Erkenntnissen über Zahlen und Rechenoperationen zu gelangen“ (Gaidoschik, 2007, S. 44).
Zahlen mit den Fingern darstellen
Bei der Arbeit mit den Fingern ist es wichtig, dass diese nicht dynamisch, d.h. zum Zählen verwendet werden, sondern dass die Kinder angeregt werden, mit Hilfe ihrer Finger Zahlen statisch – als Fingerbild – darzustellen.
An einer Hand sind fünf Finger:
Zunächst muss gesichert sein, dass alle Kinder wissen, wie viele Finger sich an einer Hand bzw. an beiden Händen befinden.
"Zähl mal deine Finger an einer Hand. Wie viele sind es?"
"Und wie viele Finger hast du an der anderen Hand? Zähl ruhig nach."
"Und wie ist das mit meiner Hand? Habe ich auch fünf Finger?"
"Jetzt schüttele ich meine Hand. Sind es immer noch fünf Finger?"
(Finger zu einer Faust ballen.) "Und jetzt? Sind es jetzt auch noch fünf Finger? Und was passiert, wenn ich meine Hand verstecke?"
Zahlen mit den Fingern darstellen:
Die Kinder werden angeregt, verschiedene Zahlen mit ihren Fingern "statisch" darzustellen. Wichtig ist hier, dass immer auch über die Zahldarstellungen gesprochen wird.
Abbildung 9
"Zeige ‚vier‘ (‚drei‘, ‚fünf‘, ...)."
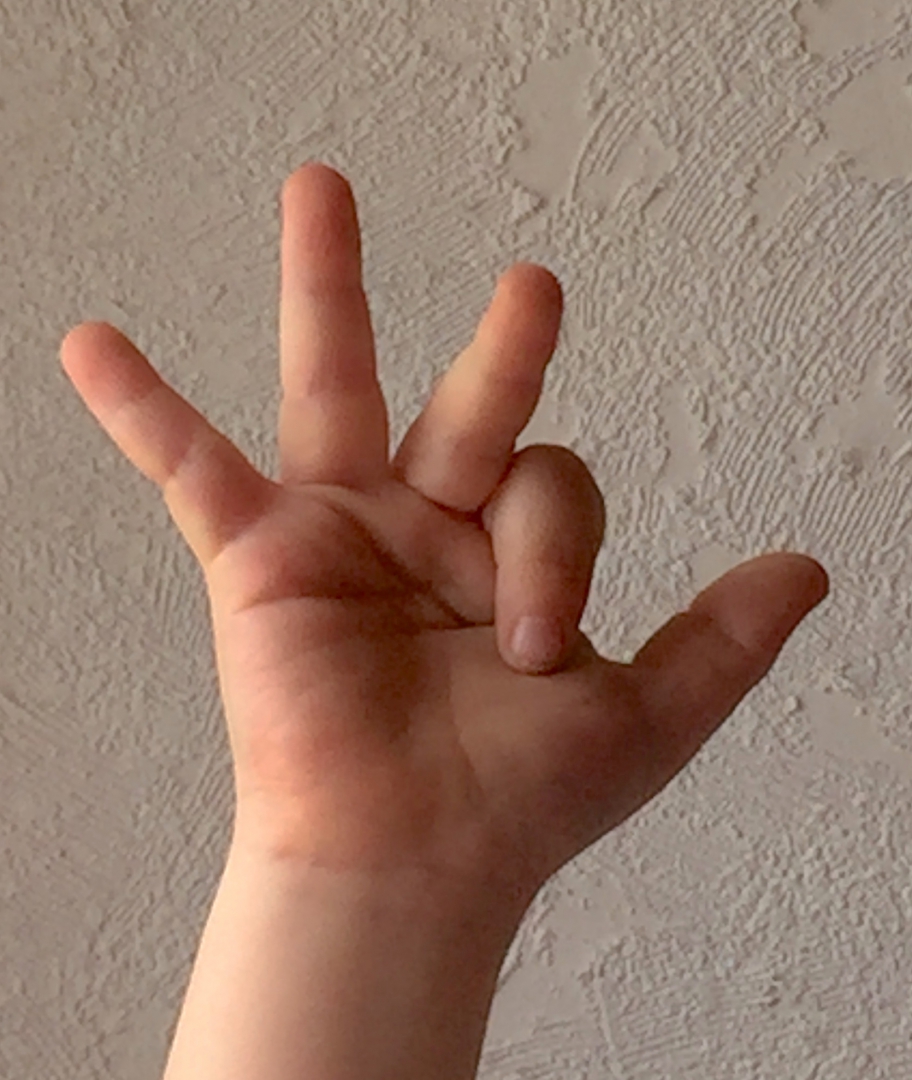Abbildung 10
"Kannst du die Zahl auch mit anderen Fingern zeigen?"
Abbildung 11
"Gibt es noch eine Möglichkeit?"
"Kannst du die Zahl auch mit zwei Händen zeigen? Wie viele Finger hast du ausgestreckt an deiner rechten Hand? Und wie viele an deiner linken Hand?"
Abbildung 12
Verschiedene Darstellungen der "vier" nebeneinander:
"Ist das immer vier? Woher weißt du das? Was fällt dir auf?"
Abbildung 13
Wichtig ist es auch, den Bezug zur fünf (oder auch zur zehn) herzustellen:
"Wie viele Finger fehlen noch bis zur fünf? Wie viele Finger musst du noch ausstrecken, bis du fünf Finger zeigst?" (Anregungen aus: Gaidoschik, 2007, S. 44)
Zahlen darstellen an Vorstrukturierten Materialien
Die vorstrukturierten Materialien bieten vielfältige Lernchancen zur Darstellung von Zahlen auf der Grundlage der angebotenen (dezimalen) Strukturierung und zielen in besonderer Weise auf den Umgang mit den dekadischen Strukturen.
Sie sichern immer einen Bezug der Darstellungen zur 5, zur 10 und zur 20 (bei größeren Anzahlen auch zur 100 oder 1000). Der Aufbau sicherer Zahlvorstellungen und Größenbeziehungen wird hierdurch unterstützt; ein bedeutsamer Aspekt bei der Prävention eines verfestigten zählenden Rechnens: "Hier wird das Verständnis des Stellenwertes, das Gliedern in Zehner vorbereitet, ohne dass hier schon explizit über Stellenwerte gesprochen wird" (Scherer, 1999, S. 162).
Um die "Kraft" der vorstrukturierten Materialien nutzen zu können und auch um diese für die Durchführung von Übungen zum „schnellen Sehen“ nutzen zu können, ist es wichtig, dass die Kinder sich zunächst intensiv und ausführlich mit den eingesetzten Materialien auseinandersetzen und die strukturellen Hintergründe der Materialien sehen und nutzen lernen. Dazu müssen sie zunächst eigenständig aktiv erkunden,
-
wie Anzahlen strukturiert dargestellt werden können,
-
wie Bündelungs- und Entbündelungsprozesse vorgenommen werden können,
-
inwiefern sich strukturierte Darstellungen von unstrukturierten unterscheiden und
-
welche Vorteile strukturierte Darstellungen besitzen.
Beispiel: Zahlen am 20er Feld
Arbeiten die Kinder mit dem 20er-Feld, müssen sie zunächst dessen Struktur erfassen: Der Rahmen des 20er-Feldes bietet Platz für 20 Plättchen, diese sind in zwei Reihen/Spalten mit jeweils 10 Punkten angeordnet. Der Zehner kann als Reihe (zwei Fünfer nebeneinander) oder als zwei Fünfer untereinander gesehen werden.
Stellen Kinder Anzahlen am 20er-Punktefeld dar, geht es immer auch um die Frage, ob das Erkennen der Gesamtzahl der Plättchen durch die Darstellung unterstützt wird.
Wichtig ist hierbei auf der einen Seite, den Kindern zunächst Freiraum zu geben für das „Erfinden“ eigener Darstellungen, Muster bzw. Punktebilder.
Abbildung 14
Auf der anderen Seite jedoch kann dann auch mit den Kindern über Verabredungen und Konventionen in Bezug auf Darstellungen am Punktefeld gesprochen werden, so dass die Anzahl der Plättchen direkt bestimmt werden kann (vgl. Scherer & Moser Opitz, 2010).
"Wenn Kinder z. B. abwechslungsweise rote und blaue Plättchen legen oder zwischen diesen Lücken lassen, kann die Regel vorgegeben werden, dass zuerst nur eine Farbe verwendet wird und dass keine Lücken gemacht werden. Es gibt auch Kinder, die beginnen ohne erkennbares Prinzip einmal in der oberen Reihe und einmal in der unteren, einmal links und einmal rechts mit dem Legen der Plättchen. Mit diesen Kindern kann nach sorgfältiger Beobachtung der Händigkeit und des dominanten Auges z. B. festgelegt werden, wo jeweils mit dem Legen der Plättchen begonnen wird“ (Moser Opitz, 2007).
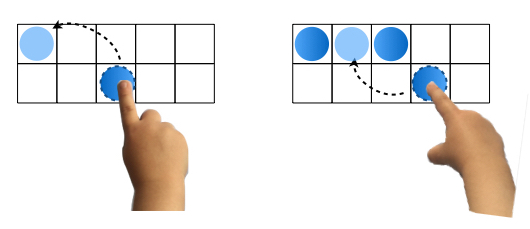Abbildung 15
Übungen zum "schnellen Sehen"
In Bezug auf den Aufbau von inneren Vorstellungen zu den verschiedenen Anzahlen stellen Übungen zum "schnellen Sehen" einen letzten Schritt dar. Das "schnelle" bzw. "blitzartige" Erkennen von Anzahlen muss trainiert und automatisiert werden. Anregungen, Ideen und Übungen hierzu finden Sie unter Unterricht: Schnelles Sehen.
Voraus gehen – wie oben bereits ausführlich erläutert – Aufgabenstellungen zur Anzahlerfassung und zur Darstellung von Anzahlen mit unstrukturierten und vorstrukturierten Materialien, denn das Material, das für die Übungen eingesetzt wird, muss den Kindern in seiner Struktur vertraut und bekannt sein. Später genügt es auch, mit Darstellungen zu arbeiten, d.h. Bilder von Punktefeldern mit eingezeichneten Punkten zu verwenden.
Zudem erfordert die strukturierte Anzahlerfassung – und insbesondere das „schnelle Sehen“ – das Wissen über die Gesamtzahl der Elemente, die sich durch das Zusammensetzen von Teilmengen ergibt. D. h. dass die Kinder bereits wissen müssen, dass beispielsweise fünf Elemente und zwei Elemente zusammen sieben Elemente ergeben. "Andernfalls müsste man die Gesamtanzahl selbst dann zählend ermitteln, wenn man die Teilanzahlen simultan erfasst hat“ (Gaidoschik, 2010, S. 217).
Der Aufbau innerer Vorstellungen zu den verschiedenen Anzahlen ist eine der Zielsetzungen der Arbeit mit dem 20er-Feld. Speziell Kinder mit besonderem Förderbedarf haben oft Schwierigkeiten, geeignete innere Bilder bzw. Vorstellungen zu Zahldarstellungen zu entwickeln. Hier muss der Prozess durch die Lehrkraft angeleitet und begleitet werden.
