 Abbildung 1 - Unterrichtsverlauf
Abbildung 1 - Unterrichtsverlauf
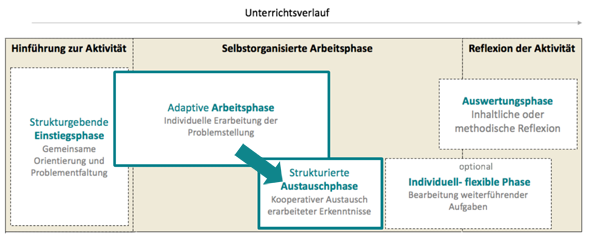
Abbildung 1 zeigt einen typisierten Unterrichtsverlauf. Die Stunde beginnt mit einer strukturgebenden Einstiegsphase, in der eine Aufgabenstellung erläutert wird. Ein Unterricht, der differenz-sensibel die unterschiedlichen Lernvoraussetzungen der Lernenden berücksichtigt, ermöglicht in der adaptiven Arbeitsphase eine individuelle Erarbeitung der Problemstellung. Das heißt auch, dass ganz unterschiedliche Arbeitsergebnisse – und zum Teil unterschiedliche Arbeitsaufträge – die Gesprächsgrundlage in der Austauschphase bilden können.
Die Herausforderung ist nun, die Austauschphase so vorzubereiten und zu strukturieren, dass trotzdem möglichst alle Schülerinnen und Schüler von diesem Austausch profitieren können.
Wie bereits dargestellt, bilden dabei die inhaltsübergreifenden Kompetenzen „Aktiv zuhören“, „Verständnis entwickeln“ und „Fehler produktiv nutzen“ wichtige Voraussetzungen. Diese werden im Folgenden mit verschiedenen Aufgabenstellungen und unterstützendem Material exemplarisch konkretisiert. Welcher Art die Auseinandersetzung mit den Ideen der Gesprächspartnerin oder des Gesprächspartners sein kann, wird dann an zwei Aufgabenstellungen gezeigt, die die „Ebenen der Auseinandersetzung“ verdeutlichen sollen.
Aktiv zuhören
Um die Lernenden darin zu unterstützen, ihrer Partnerin oder ihrem Partner aktiv zuzuhören, kann schon viel durch die Aufgabenstellung sowie die Strukturierung der Austauschphase erreicht werden. Trotzdem benötigen Lernende Zeit und Erfahrung, um einschätzen zu können, „was auf sie zukommt“ und was für sie persönlich beim Zuhören wichtig ist und was nicht.
 Abbildung 2 - Nachbarn auf dem 20er-Feld
Abbildung 2 - Nachbarn auf dem 20er-Feld
Bei dieser Aufgabe, angelehnt an die Lernumgebung „Wir erforschen Nachbarzahlen und ihre Summen“ (Korten, 2020, 151), sollen die Lernenden gemeinsam alle Nachbarn auf dem 20er-Feld finden und ihre Summen berechnen, wobei ein Partner horizontale Nachbarn (A: schwer), der oder die andere vertikale Nachbarn (B: leicht) finden soll. Dies differenziert zum einen
-
In der Menge: horizontale Nachbarn: 18 Paare; vertikale Nachbarn: 10 Paare, sowie
-
in der Schwierigkeit der Aufgaben: horizontale Nachbarn: auch Aufgaben vom Typ 17+18; vertikale Nachbarn: Aufgaben vom Typ 13+3, 17+7.
Zusätzlich sollen mit Hilfe von Forschermitteln mögliche Entdeckungen dokumentiert werden. Es folgt ein gemeinsamer Arbeitsauftrag, der sowohl die Austauschphase strukturiert, als auch beide sich ergänzenden Aufträge zusammenführt.
 Abbildung 3 - Nachbarn auf dem 20er-Feld - Team
Abbildung 3 - Nachbarn auf dem 20er-Feld - Team
Zieltransparenz
Die sich ergänzende Aufgabenstellung begünstigt eine positive extrinsische Abhängigkeit, es gibt ein gemeinsames Ziel („Findet geschickt alle Nachbarn auf dem 20er-Feld und berechnet ihre Summen!“), das durch die Zusammenlegung beider Arbeitsergebnisse erreicht werden kann.
Damit die Lernenden wissen, auf was sie beim Zuhören achten sollen, sollte der Auftrag „Wiederholt danach mit euren Worten, was eurem Partner aufgefallen ist!“ vor der Austauschphase gelesen werden.
Aktivierung des Vorwissens
Die Lernenden haben die Möglichkeit, sich in einer individuellen Arbeitsphase mit dem Thema „Nachbarn auf dem 20er-Feld“ zu beschäftigen. Durch die Ähnlichkeit der Arbeitsaufträge wird unterstützt, dass die Entdeckungen der Partnerin / des Partners zu den eigenen Entdeckungen in Beziehung gestellt werden können.
Fähigkeit zur Aufmerksamkeitssteuerung
Das Arbeitsblatt „Nachbarn auf dem 20er-Feld (Team)“ (Abb. 5) strukturiert die Austauschphase (Aufg. 1 und 2) durch die Festlegung von Themen. Außerdem unterstützt die feste Rollenzuschreibung durch die Rollenkarten die Phasen des Dialogs.
Regeln für Partnergespräche
Zusätzlich wird ein Hinweis auf die „Regeln für Partnergespräche“ gegeben. Diese sollten an die Bedürfnisse der Lerngruppe angepasst mit den Schülerinnen und Schülern gemeinsam erarbeitet werden. Ein gutes Beispiel für Gesprächsregeln findet sich bei:PIKAS: Plakate KommunikationPIKAS: Haus 8: Guter Unterricht – Unterrichtsmaterial – Kommunikation fördern.
 Abbildung 4 - PIKAS: Plakate Kommunikation
Abbildung 4 - PIKAS: Plakate Kommunikation
Verständnis entwickeln
Die Schülerinnen und Schüler sollen motiviert werden, sich in die Partnerin oder den Partner hineinzuversetzen, besonders wenn diese / dieser ein anderes Arbeitsergebnis oder sogar einen abweichenden Arbeitsauftrag mitbringt. Dieses „Sinn suchen“ in den Lösungen eines Partnerkindes kann im „normalen“ Unterricht immer wieder und auch ohne vorangegangene Austauschphase trainiert werden.
 Abbildung 5 - Aufgaben zu "Verständnis entwickeln"
Abbildung 5 - Aufgaben zu "Verständnis entwickeln"
In diesem Beispiel beschäftigt sich einer der Lernenden (A) mit Mal-Aufgaben, während sein Partner / seine Partnerin (B) mit Plus-Aufgaben arbeitet. Nachdem beide Lernenden sich auf ein Punktefeld geeinigt haben, mit dem sie arbeiten möchten, schreibt Partner A Mal-Aufgaben, Partner B Plusaufgaben dazu auf. Danach haben sie die Aufgabe herauszufinden, welche Stelle des Punktefelds zu den Aufgaben des Partners / der Partnerin passen. Das Punktefeld dient dabei sowohl als Darstellungsmittel, mit dessen Hilfe konkreter kommuniziert werden kann, als auch als Anschauungsmaterial, das die Operationsvorstellungen der Addition und Multiplikation verdeutlicht.
Die Aufgabe kann mit wenig Aufwand erweitert werden, z. B., indem mehr Punktefelder angeboten werden oder sich zu Beginn nicht auf ein Punktefeld geeinigt wird.
Die Grundidee der Aufgabe „Ich versuche die Lösung eines Partners zu interpretieren und komme darüber mit ihm ins Gespräch.“ lässt sich auf nahezu jeden Aufgabentyp übertragen, der nicht auf das bloße Lösen einer Rechenoperation beschränkt ist.
Fehler produktiv nutzen
Ganz ähnlich, wie beim „Verständnis entwickeln“ geht es auch an dieser Stelle zunächst darum, in den Lösungen des Partnerkindes nach „Sinn“ zu suchen, selbst wenn dieses einen Fehler gemacht hat. Entscheidend ist, dass die Schülerinnen und Schüler dabei lernen, Fehler als Chance und produktiven Gesprächsanlass wahrzunehmen. Die Lernenden können von Impulsen der Lehrkraft und Formulierungshilfen unterstützt werden.
In dem hier vorgestellten Beispiel (nach Schulz und Benz, 2019) können die Lernenden sowohl die Fehleranalyse, als auch das Formulieren hilfreicher Tipps zunächst trainieren, ohne dass der Fehler tatsächlich einem Kind in der Klasse passiert sein muss.
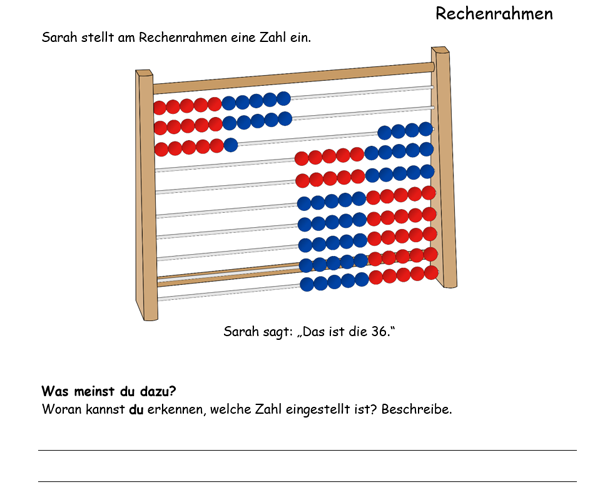 Abbildung 6 - Aufgabenstellung Fehler produktiv nutzen - Rechenrahmen
Abbildung 6 - Aufgabenstellung Fehler produktiv nutzen - Rechenrahmen
Von Vorteil ist dabei, dass sich die Aufgabenstellung auf das Verständnisproblem eines Anschauungsmittels bezieht. Dies erleichtert es den Schülerinnen und Schülern, die dahinterliegende Fehlvorstellung aufzudecken und zu beschreiben. Dafür wird zunächst die eigene Vorstellung „aktiviert“: „Woran kannst du erkennen, welche Zahl eingestellt ist? Beschreibe.“ Anschließend soll die Perspektive von Sarah eingenommen werden „Was hat sich Sarah vielleicht gedacht?“ und ihr geholfen werden, diese zu überwinden „Welchen Ratschlag gibst du Sarah?“.
Auch diese Grundidee lässt sich leicht auf andere Formate übertragen, in denen Anschauungsmittel genutzt werden, z.B.
Ebenen der Auseinandersetzung
Um die aktive Auseinandersetzung mit den Äußerungen der Gesprächspartnerin oder des Gesprächspartners anzuregen, sind im vorherigen Kapitel verschiedene Impulse formuliert worden, die sich den Ebenen „Wiedergeben“, „Vergleichen“ und „Reflektieren“ zuordnen lassen. Je nach Aufgabenstellung und Lernvoraussetzungen der Lernenden können unterschiedliche Impulse sinnvoll sein.
Grundsätzlich gilt aber, dass
-
von „Wiedergeben“ über „Vergleichen“ bis „Reflektieren“ der Anspruch an die Kompetenzen der/ des Lernenden steigt, genauso, wie die inhaltliche Tiefe der Auseinandersetzung,
-
trotzdem alle Kinder grundsätzlich auch alle Ebenen der Auseinandersetzung einnehmen können, wenn der mathematische Inhalt zu den Lernvoraussetzungen des Kindes passt.
Dadurch können sich, je nach Zusammensetzung der Gesprächspartnerschaft, unterschiedliche Konstellationen ergeben, die jeweils eine individuelle Auseinandersetzung mit den Äußerungen der Partnerin / des Partners ermöglicht.
Beispielsweise kann ein mathematischer Inhalt, der noch nicht sicher beherrscht wird, zunächst einfach von der Partnerin/ vom Partner imitiert werden (z. B. im Stellenwertsystem: „Zähle wie dein Partner: 10, 20, 30, …“). Umgekehrt kann ein Perspektivwechsel („Was hat sich dein Partner dabei gedacht?“) oder ein Kontextwechsel („Funktioniert das auch mit Zahlen über 20?“) eher von Kindern vorgenommen werden, wenn sie sich sicher im Zahlenraum bewegen und über ausreichend Erfahrungen mit dem mathematischen Inhalt verfügen.
Analog zum Teilmodul „Sich verständlich machen“ wird auch hier wieder zwischen Aufgabenstellungen unterschieden, die ein bestimmtes Arbeitsergebnis, Arbeitsprodukt oder eine Entdeckung fokussieren und Aufgabenstellungen, die ein bestimmtes Vorgehen oder einen Lösungsweg in den Vordergrund rücken.
Auseinandersetzen mit Produkten
 Abbildung 7 - Aufgabenbeispiel Produkte
Abbildung 7 - Aufgabenbeispiel Produkte
Die Grundlage für dieses Aufgabenbeispiel stellen die Quadratzahlaufgaben aus „Aufgaben adaptieren“ dar. Hier sollen auf einem 100er-Feld jeweils aufeinanderfolgende Mal-Aufgaben mit gleichen Faktoren ausgerechnet und Entdeckungen dazu dokumentiert werden.
 Abbildung 8 - Aufgabenbeispiel Produkte - Team
Abbildung 8 - Aufgabenbeispiel Produkte - Team
Auch hier sollen sich die Lernenden zunächst nacheinander ihre Entdeckungen erklären, dabei die Forschermittel (PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Unterrichtsmaterial – Forschermittel-Plakat) zur Hilfe nehmen und die Gesprächsregeln beachten. Danach folgen Aufgaben zur Rekapitulation (Aufgabe 2) und zum Vergleichen (Aufgabe 3). In Aufgabe 4 wird durch die Erweiterung des Zahlenraums („Findet ihr noch 3 Quadratzahlen…?“) ein Kontextwechsel angeregt. Bezogen auf die Aufgabe 3 des vorherigen Arbeitsblatts (Abb. 11), wäre auch ein Perspektivwechsel („Warum denkt dein Partner, dass diese Zahlen Quadratzahlen heißen?“) möglich.
Gesprächsregeln
Auseinandersetzen mit Vorgehensweisen
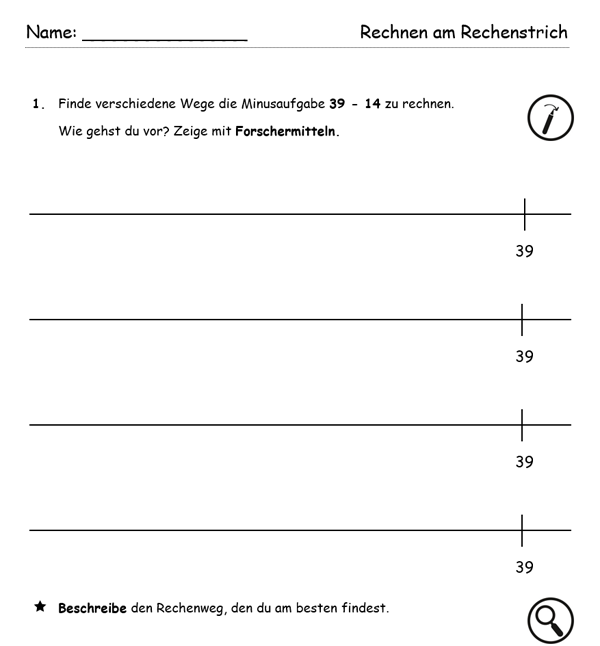 Abbildung 9 - Aufgabenbeispiel Vorgehensweisen
Abbildung 9 - Aufgabenbeispiel Vorgehensweisen
Verschiedene Rechenwege für eine Aufgabe zu finden, zu beschreiben und Favoriten auszuwählen, ist gerade im gemeinsamen Austausch sinnvoll. Auch die hier vorgestellte Aufgabe stammt aus dem Bereich „Aufgaben adaptieren“. Sie zeichnet sich unter anderem dadurch aus, dass sie durch eine Anpassung des Zahlenraumes gut zu differenzieren ist. Durch das verbindende Anschauungsmittel „Rechenstrich“ können Lernende mit heterogenen Lernvoraussetzungen analoge Vorgehensweisen beschreiben und der gemeinsame Austausch wird erleichtert.
 Abbildung 10 - Aufgabenbeispiel Vorgehensweisen - Team
Abbildung 10 - Aufgabenbeispiel Vorgehensweisen - Team
Nachdem die Lernenden sich in Aufgabe 1 ihre Rechenwege, sowie ihren „Lieblingsweg“ vorgestellt haben, folgt mit Aufgabe 2 eine Imitation des Rechenwegs der Partnerin oder des Partners. Die Aufgabe 3 regt zu einem Wechsel der Perspektive an, indem nach einer Bewertung des Rechenwegs aus Sicht des Partners bzw. der Partnerin gefragt wird. Aufgabe 4 stellt hingegen einen Impuls zum Kontextwechsel dar, indem das Anschauungsmittel getauscht wird.