Wie bereits im vorangegangenen Modul „Vorerfahrungen berücksichtigen“ dargestellt wurde, ist mathematisches Lernen immer auch ein Weiterlernen. „Auf Vorwissen und den bereits erlernten Konzepten und Vorstellungen wird sukzessive aufgebaut, es wird vernetzt, und Zusammenhänge werden hergestellt. Gibt es in diesem Lernprozess Lücken, die nicht erkannt werden, so ist die Gefahr groß, dass sich Schwierigkeiten beim Weiterlernen ergeben“ (Hasemann und Gasteiger, 2014, 51).
Spiralprinzip
Lernen erfolgt aber nicht nur in der Rück-, sondern auch in der Vorschau: Genauso, wie auf Gelerntem aufgebaut wird, führt Lernen immer auch zu neuen Inhalten, Vorstellungen oder Erkenntnissen hin. Aus diesem Grund sollten Lernprozesse im Unterricht langfristig angelegt und so gestaltet werden, dass auch in späteren Phasen ein kontinuierliches Weiterlernen ohne größere Brüche möglich ist.
Diesem Anspruch wird das Spiralprinzip (Bruner, 1997) gerecht, indem
-
grundlegende mathematische Inhalte (z.B. Symmetrie, Zahlreihen, Rechengesetze, Zehnersystem, ...),
-
Darstellungsmittel (z.B. Punktefelder zur Darstellung der Multiplikation, zur Darstellung von Rechengesetzen, …)
-
Aufgabenformate und Aufgabenstellungen (z. B. Zahlenmauern, Entdeckerpäckchen, ...)
in den einzelnen Schuljahren wiederkehrend aufgegriffen, daran bewusst angeknüpft und das bereits bestehende Wissen vertieft werden (Schwätzer, 2009, S. 554).
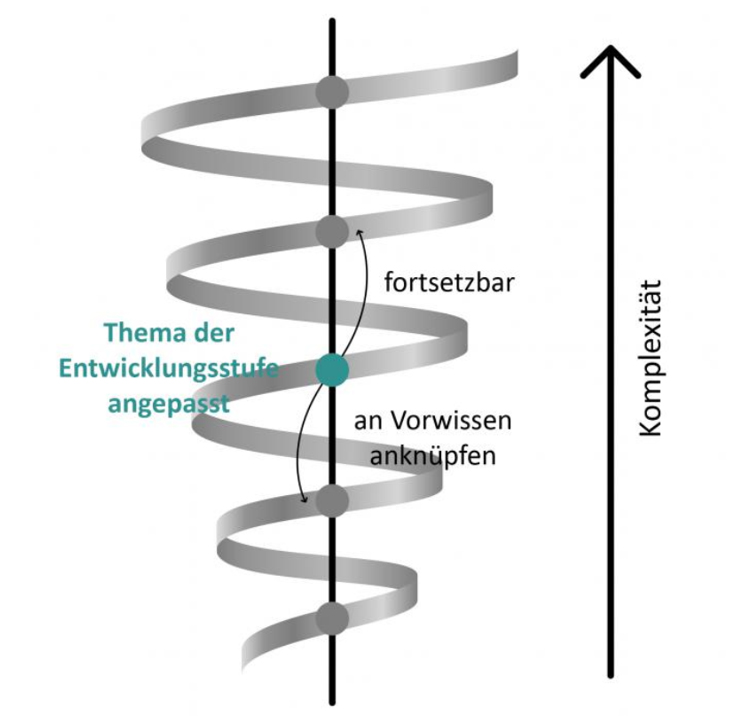
Abbildung 1: Spiralprinzip (primakom.dzlm.de/node/261)
Dabei werden die Themen an die jeweilige Entwicklungsstufe der Kinder angepasst (siehe Abbildung 1 – Spiralprinzip). Hierbei ist sowohl entscheidend, dass vorhandenes Vorwissen aufgegriffen wird, als auch, dass neues Wissen in späteren Lernphasen fortsetzbar ist. Außerdem werden „mit dem Fortschreiten auf der ‚Spirale’ anfangs intuitive, ganzheitliche, undifferenzierte Vorstellungen zunehmend von formalen, deutlicher strukturierten, analytisch durchdrungenen Kenntnissen überlagert“ (Müller & Wittmann, 1984, S. 157).
Wie Lernprozesse im Sinne des Spiralprinzips kontinuierlich angelegt können, wird nun beispielhaft für grundlegende mathematische Inhalte, Darstellungsmittel und Aufgabenformate und Aufgabenstellungen illustriert.
Kontinuität grundlegender mathematischer Inhalte
Grundlegende Inhalte, die Lernende erwerben sollen, werden beispielsweise in der Fachliteratur formuliert (z.B. Winter 2001) und finden sich in Form von Kompetenzerwartungen in den jeweiligen Lehrplänen für Mathematik.
So kann beispielsweise der Inhalt „Symmetrie“ an die einzelnen Entwicklungsstufen der Kinder angepasst werden. Im Folgenden wird dies theoretisch beschrieben und im Unterrichtsteil dann praktisch anhand von Aufgabenbeispielen veranschaulicht.
Auch wenn es in NRW für KiTas keinen verbindlichen Bildungsplan gibt, soll Kindern laut den Bildungsgrundsätzen (MSB & MKFFI NRW, 2018) die Möglichkeit gegeben werden „einfache Muster zu entdecken und zu beschreiben und Regelmäßigkeiten (Ornamente, Bodenfliesen, gelegte Plättchenreihen etc.) fortzusetzen oder selbst herzustellen“ (ebd., S. 117).
In der Schuleingangsphase werden diese ersten Zugänge zu Mustern fortgesetzt: „Die Schülerinnen und Schüler identifizieren bei einfachen ebenen Figuren Eigenschaften der Achsensymmetrie (u.a. durch Klappen, Durchstechen, Spiegeln mit dem Spiegel)“ (MSB NRW 2021, 91) und sollen dann bis zum Ende der Grundschulzeit ausgebaut werden: „Die Schülerinnen und Schüler fertigen symmetrische Figuren an (u. a. Zeichnen von Spiegelbildern auf Gitterpapier, Spiegeln mit einem Doppelspiegel) und nutzen dabei die Eigenschaften der Achsensymmetrie, auch unter Verwendung digitaler Mathematikwerkzeuge“ (MSB NRW 2021, 91). Die Kompetenzerwartungen werden hier insofern abstrakter, dass diese von einem „Identifizieren von Eigenschaften“ zum „Anfertigen“, aber auch das Arbeiten mit konkreten Materialien (Klappen, Durchstechen) zum Zeichnen auf Gitterpapier erweitert wird.
In der Sekundarstufe 1 – hier beispielsweise an der Gesamtschule am Ende der Jahrgansstufe 6 – werden die Begriffe dann erweitert: „Schülerinnen und Schüler verwenden die Grundbegriffe […] achsensymmetrisch, punktsymmetrisch zur Beschreibung ebener und räumlicher Figuren“ (MSB NRW 2004, S. 21). Es wird also eine weitere Eigenschaft der Symmetrie ergänzt.
Somit wird deutlich, dass grundlegende Inhalte über die Schuljahre hinweg immer wieder thematisiert werden, einerseits, um den Lernenden einen anschlussfähigen Wissensaufbau zu ermöglichen und andererseits um ihr Vorwissen immer wieder aufzugreifen und zu erweitern. Dabei sollen zunächst eher intuitive, ganzheitliche und undifferenzierte Aktivitäten von zunehmend strukturierten, formalen und analytisch geprägten Vorgehensweisen abgelöst werden (Müller & Wittmann, 1984, S. 157).
Kontinuität der Darstellungsmittel
Darstellungsmittel spielen im Lernprozess eine entscheidende Rolle, etwa beim Aufbau von Grundvorstellungen und mentalen Bildern, aber auch als Anschauungs- oder Arbeitsmittel. Sie sind damit einerseits Lernhilfe, andererseits aber immer auch Lerngegenstand selbst. Ein entscheidendes Qualitätskriterium ist dabei, inwieweit die an den Darstellungsmitteln erarbeiteten Grundvorstellungen tragfähig sind, sie also in den folgenden Schuljahren erweitert werden können. Dies kann am Beispiel des Darstellungsmittels „Punktefeld“ zur Operationsvorstellung der Multiplikation illustriert werden.
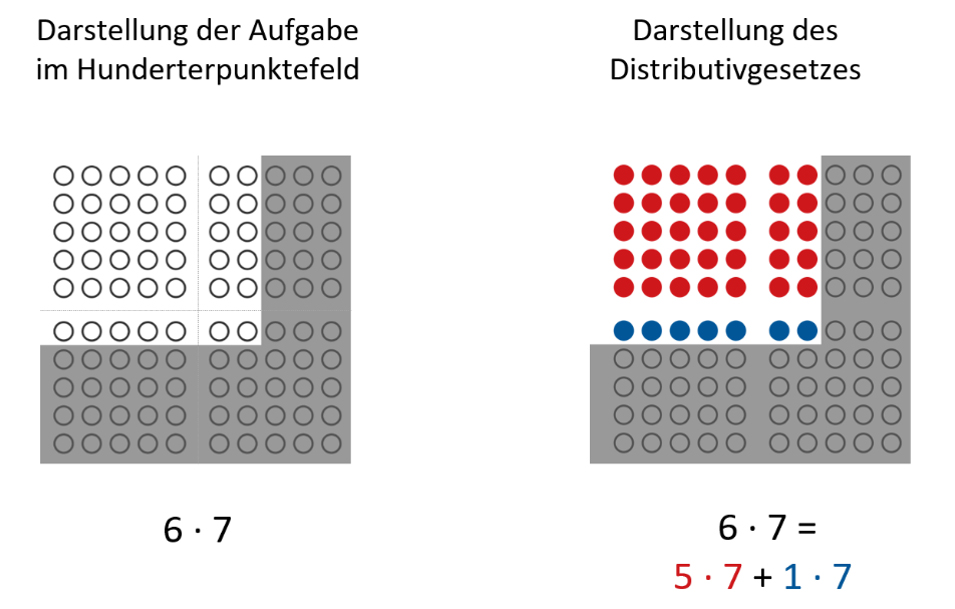
Abbildung 2: 6 mal 7 im Hunderterpunktefeld
Das Punktefeld zur Aufgabe „6 ∙ 7“ kann mithilfe einer Schablone als Ausschnitt des Hunderterpunktefelds dargestellt und gesehen werden (Abbildung 2). Die farbliche Markierung der Punkte im Hunderterpunktefeld veranschaulicht – unter anderem – die Anwendung des Distributivgesetzes: die Aufgabe „6 ∙ 7“ kann auch als „5 ∙ 7 + 1 ∙ 7“ gesehen werden.
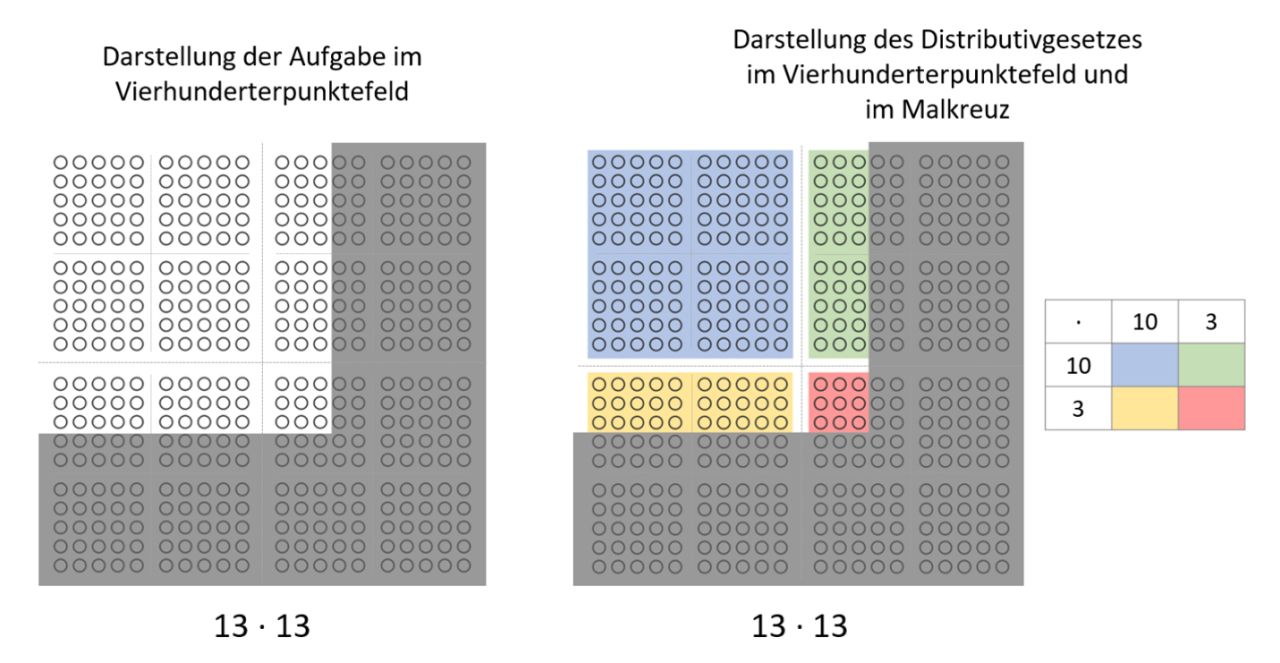 Abbildung 3: Multiplikation, Distributivgesetz und Malquadrat
Abbildung 3: Multiplikation, Distributivgesetz und Malquadrat
Die Darstellung der Multiplikation am Punktefeld kann auch auf größere Zahlenräume übertragen werden, etwa bei der Aufgabe „13 ∙ 13“, die dann im Vierhunderterpunktefeld dargestellt wird (Abbildung 3). Die farbliche Markierung der Punkte veranschaulicht wiederum die Anwendung des Distributivgesetzes. Zusätzlich kann die analog eingefärbte Darstellung im Malkreuz ein Verständnis der gestützten Multiplikation unterstützen.
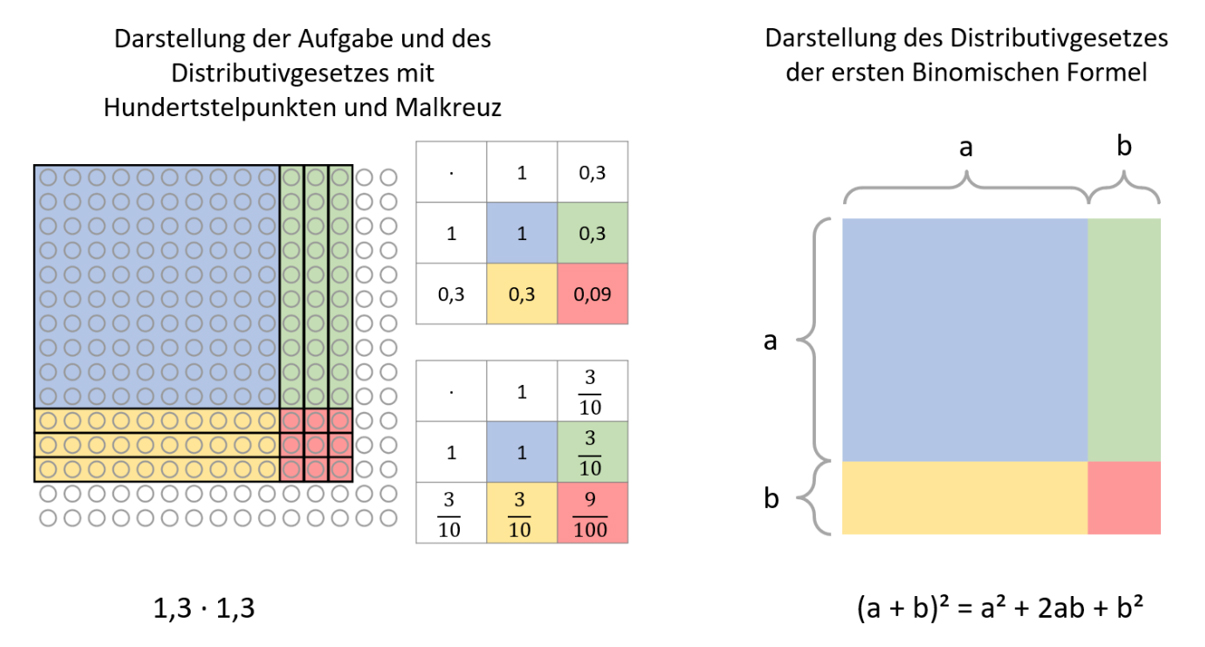
Abbildung 4: Multiplikation von Dezimalbrüchen, erste binomische Formel
Auch in der Sekundarstufe kann auf die Darstellung der Multiplikation am Punktefeld zurückgegriffen werden. Wenn bei der Erweiterung des Zahlenraums auch Dezimalbrüche multipliziert werden, kann durch eine entsprechende Darstellung auch die Operationsvorstellung der Multiplikation erweitert werden. Die Visualisierung des Distributivgesetzes ermöglicht außerdem bspw. ein tieferes Verständnis der Multiplikation mit Variablen, dargestellt ist hier die erste binomischen Formel.
Kontinuität der Aufgabenformate und Aufgabenstellungen
Auch Aufgabenformate und Aufgabenstellungen können immer wieder unter neuen Gesichtspunkten auf verschiedenen Entwicklungsstufen aufgegriffen werden. Ziel ist die zunehmende Integration weiterer oder neuer Konzepte, Ideen oder Fertigkeiten (Krauthausen, 2016, S. 32), wobei gerade auch prozessbezogene Kompetenzen systematisch weiterentwickelt werden können. Dies gelingt insbesondere dann, wenn im Mathematikunterricht – angefangen in der Primarstufe – von den Lernenden durchgängig eingefordert wird, zu dokumentieren „was ihnen auffällt“ oder „wie sie etwas gemacht haben“ oder zu erklären „warum das so ist“. Lernenden fällt dies dann auch bei schwierigeren oder noch unbekannten Inhalten immer leichter, weil diese prozessbezogenen Kompetenzen immer wieder gefordert und somit gefördert werden.
Ein weiterer Vorteil besteht darin, dass nicht ständig ein neues Format eingeführt werden muss, sondern die Lernenden Aufgabenformate wiedererkennen und der Fokus schneller auf den fachlichen Inhalt gelegt werden kann. Gerade unsicheren Lernen bieten gewohnte Aufgabenformate Sicherheit, die helfen kann, sich auf neue Themen einzulassen.
Aus der Vielzahl der Aufgabenformate, die im Mathematikunterricht im Primarbereich vorkommen, werden zur Illustration hier die „schönen Päckchen“ ausgewählt. Schöne Päckchen (auch „Entdecker-Päckchen“ genannt, weitere Informationen zu diesem Aufgabenformat z.B. bei primakom) werden im Mathematikunterricht in der Primarstufe häufig eingesetzt, um das beziehungsreiche Denken der Kinder zu fördern.
Schöne Päckchen bestehen aus operativen Aufgabenserien: gleichmäßige Veränderungen einer oder mehrerer Zahlen im Term bewirken gleichmäßige Veränderungen oder eine Konstanz der Ergebnisse. Die Kinder können dazu angeregt werden, die Muster in den Aufgabenserien zu entdecken, zu beschreiben, sie fortzusetzen oder eigene Muster zu erfinden. Aus diesen Entdeckungen wiederum können Rechengesetze, -vorteile oder -strategien entwickelt werden.
Entscheidend für solche reichhaltigen mathematischen Aktivitäten sind jedoch nicht die Aufgabenformate an sich, sondern die damit verbundenen Aufgabenstellungen, die je nach Ziel unterschiedliche prozessbezogene Kompetenzen fokussieren können (s. Abbildung 5).
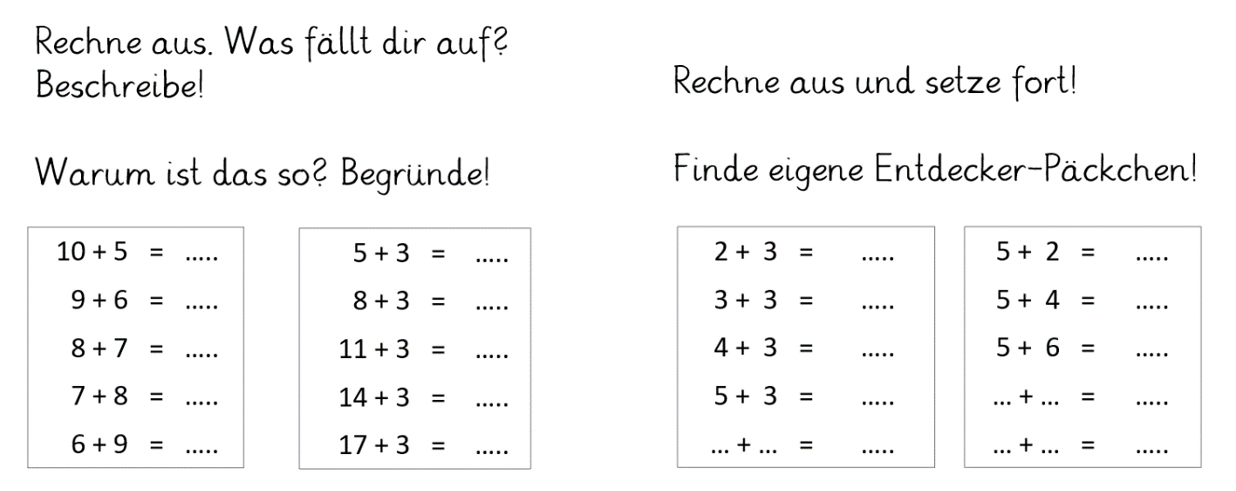
Abbildung 5: Mögliche Aufgabenstellungen für schöne Päckchen
Hier soll nun gezeigt werden, dass schöne Päckchen als langfristig angelegtes Aufgabenformat mit den entsprechenden Aufgabenstellungen auch in der Sekundarstufe aufgegriffen und gewinnbringend eingesetzt werden können (siehe Abbildung 6).
 Abbildung 6: Schöne Päckchen in der Sekundarstufe (in Anlehnung an Prediger, 2008, S.1)
Abbildung 6: Schöne Päckchen in der Sekundarstufe (in Anlehnung an Prediger, 2008, S.1)
Analog zu den Aufgaben in der Primarstufe können auch hier Muster in den Aufgabenserien entdeckt, fortgesetzt, beschrieben und begründet werden, wodurch potentiell tiefere Einsichten wahrscheinlicher werden, als wenn nur unverbundene Aufgaben ausgerechnet werden sollen. Schöne Päckchen eignen sich aber auch, um ganz gezielt Einsichten zu ermöglichen, etwa bei der Zahlbereichserweiterung: „Wer Vertrauen gefasst hat, in die Fortsetzbarkeit solcher Päckchen, kann sich damit auch unvertrauteren Zahlbereichen nähern“ (Prediger 2008, 3). Hierbei können offene (s. Abbildung 7, links) und zielgerichtetere (s. Abbildung 7, rechts) Aufgabenstellungen unterschiedliche prozessbezogene Kompetenzen fördern.
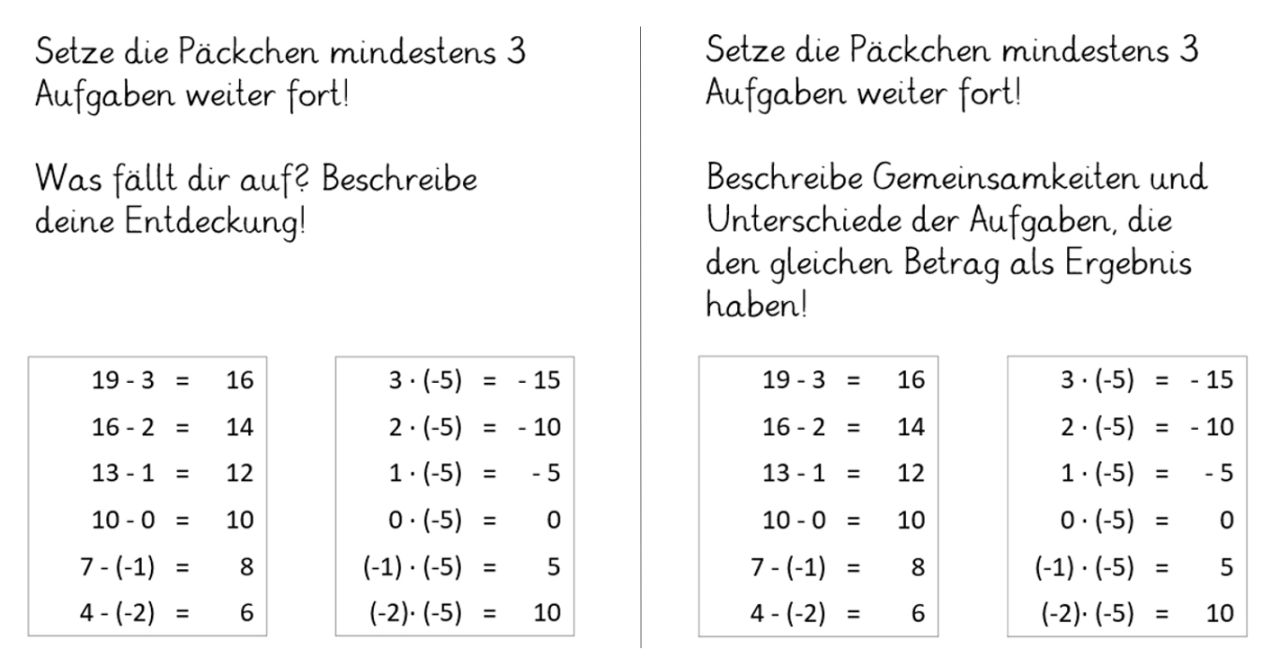
Abbildung 7: Schöne Päckchen mit negativen Zahlen, links mit offener, rechts mit zielgerichteter Aufgabenstellung (in Anlehnung an Prediger, 2008, S. 3)
Die Struktur schöner Päckchen eignet sich außerdem dazu, algebraisches Denken anzubahnen, da die Veränderungen und Zusammenhänge zwischen den Aufgaben fokussiert werden (Prediger, 2008, 3). Es geht um die Frage, wie sich die Zahlen miteinander verändern, wenn sowohl vertikale als auch horizontale Zusammenhänge (s. Abbildung 8) in den Blick genommen werden. Die Frage nach der 17 als Startzahl bahnt zusätzlich das Denken in allgemeinen, also variablen Zahlen an.
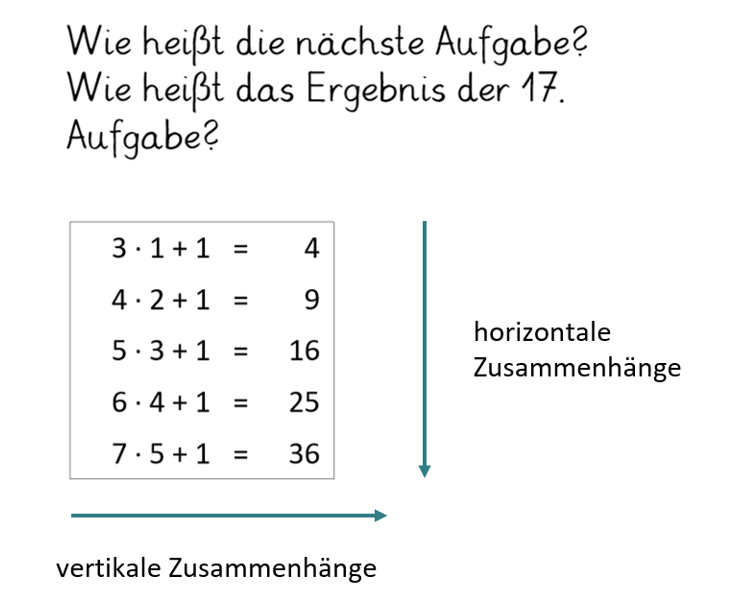
Abbildung 8: algebraisches Denken in schönen Päckchen (in Anlehnung an Prediger, 2008, S. 3)
Konsequenzen für den inklusiven Mathematikunterricht
Bei der längerfristigen Planung des Mathematikunterrichts in inklusiven Lerngruppen ergeben sich aus dem Spiralprinzip einige Konsequenzen:
Vorerfahrungen der Lerngruppe berücksichtigen
Um die Vorerfahrungen der Lerngruppe zu einem Thema berücksichtigen zu können, müssen diese grundsätzlich erhoben werden. Dabei ist besonders darauf zu achten, ob einzelnen Kindern unverzichtbare Verstehensgrundlagen fehlen, ohne die ein verständiges Weiterlernen nicht möglich ist (siehe hierzu „Vorerfahrungen berücksichtigen“).
Hinzukommt, dass mit dem neuen Unterrichtsinhalt an die Vorerfahrungen der Lernenden angeknüpft werden soll. Um dies zu ermöglichen, können die folgenden Planungsfragen sinnvoll sein:
-
Über welche Begriffe aus der Alltags- und Fachsprache verfügen die Lernenden bereits und welche Bedeutung verknüpfen sie mit ihnen?
-
Mit welchen Darstellungsmitteln haben die Lernenden in der Vergangenheit zu diesem Thema gearbeitet?
-
Welche (Grund-)Vorstellungen besitzen die Lernenden zu diesem Thema?
-
Welche Aufgabenformate und Aufgabenstellungen kennen die Lernenden bereits, die für dieses Thema relevant sein könnten?
Über die Jahrgangsstufen hinausdenken
Guter inklusiver Mathematikunterricht versucht, eine möglichst große Kontinuität in den individuellen Lernprozessen der Schülerinnen und Schülern zu ermöglichen. Gerade für Kinder mit Schwierigkeiten im Mathematiklernen halten größere Umbrüche, wie der Schul- oder Klassenwechsel, aber auch kleinere Umbrüche, wie der Einstig in ein neues Thema besondere Herausforderung bereit.
Wie im Einstiegsbeispiel dargestellt, kommt es insbesondere für Kinder mit Schwierigkeiten im Mathematiklernen immer wieder vor, dass sehr spezielle Ansätze und Darstellungsmittel genutzt werden, in der vermeintlich guten Absicht, etwas „anderes“ als den „herkömmlichen“ Mathematikunterricht anzubieten.
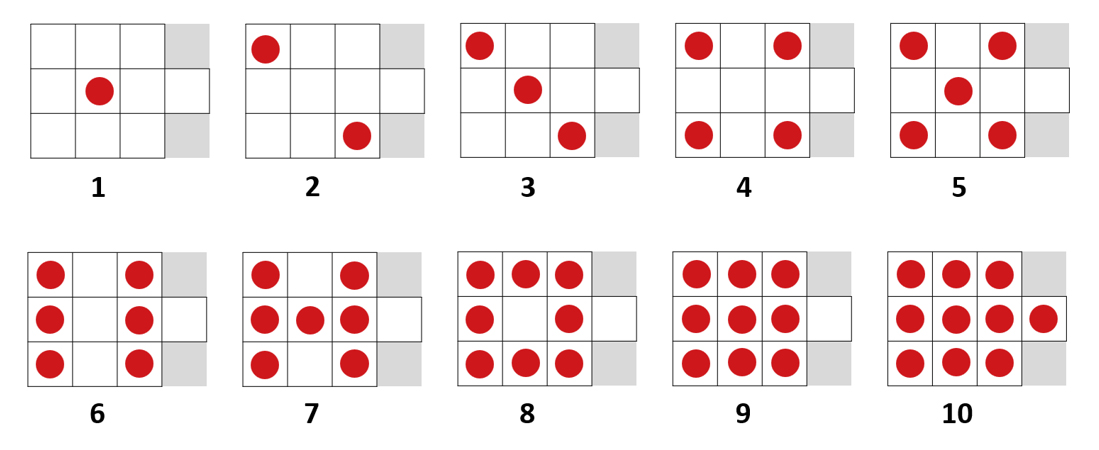
Abbildung 9: strukturierte Punktedarstellung der Zahlen 1 bis 10
Im Gegensatz zu allgemein üblichen Darstellungen wird bei den Darstellungen aus dem Einstiegsbeispiel (Abbildung 9) nicht die „Kraft der Fünf“ und die dezimale Struktur unseres Zehnersystems veranschaulicht. Dadurch lässt sich die Darstellung nicht analog zu unserem Dezimalsystem auf größere Zahlenräume erweitern (Abbildung 10).
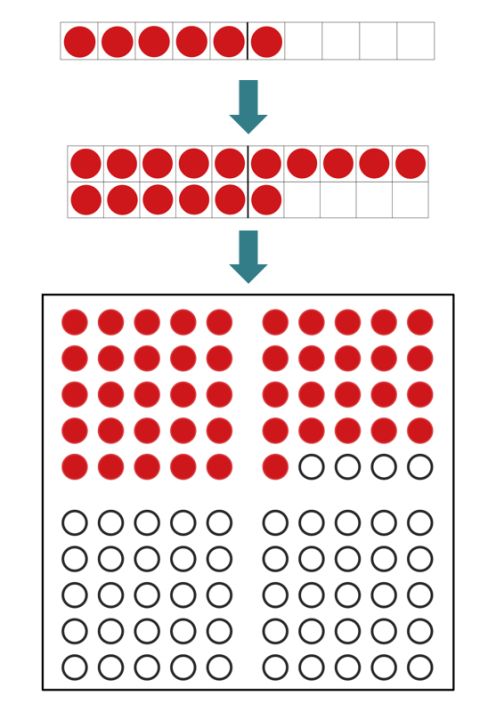
Abbildung 10: analog zum Dezimalsystem erweiterbare Zahlenfelder
Selbst wenn die Kinder also lernen, die Zahlen von 1-10 anhand der oberen Darstellung (Abbildung 9) schnell, „auf einen Blick“ zu erkennen, bleibt fraglich, welcher Nutzen dadurch für spätere Lernprozesse entsteht.
Auf die Kontinuität grundlegender Inhalte, Darstellungen und Aufgaben sollte deshalb insbesondere in inklusiven Lerngruppen Wert gelegt werden.
Differenzierung von grundlegenden Inhalten, Darstellungsmitteln, Aufgaben
Wenn Inhalte, Darstellungsmittel und Aufgaben gemäß Spiralprinzip über die Jahrgangsstufen hinweg immer wieder aufgegriffen werden, können sich für den Unterricht in heterogenen Lerngruppen Möglichkeiten der Differenzierung ergeben. So können zum Beispiel mit dem Aufgabenformat „Zahlenmauern“ in unterschiedlichen Zahlenräumen ähnliche Entdeckungen gemacht werden (siehe Abbildung 11, Aufgaben adaptieren – Verwandte Aufgaben).
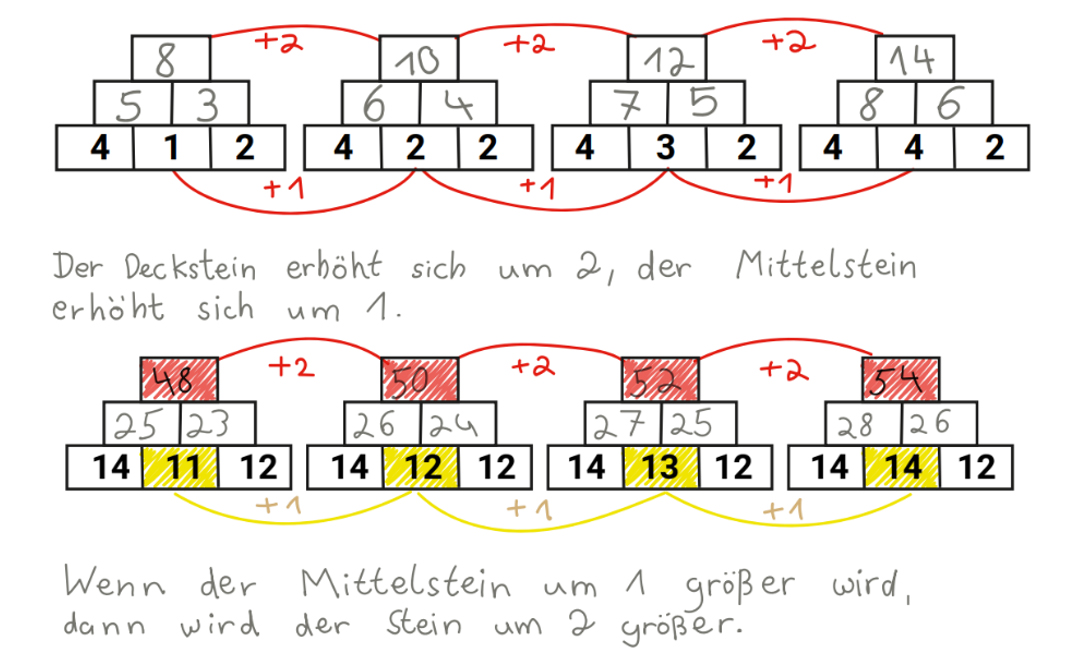 Abbildung 11: Differenzierung mit dem Aufgabenformat "Zahlenmauern"
Abbildung 11: Differenzierung mit dem Aufgabenformat "Zahlenmauern"
Auch die unter der Rubrik Inhalte auf dieser Seite bereitgestellten „Aufgabenstellungen kompakt“ sind auf verschiedenen Niveaustufen konzipiert, so dass sie entweder zur gleichen Zeit in einer heterogenen Lerngruppe durchgeführt werden können, oder zu unterschiedlichen Zeitpunkten im Entwicklungsprozess der Lernenden.