Digital gestütztes Lernen – Gemeinsam lernen mit der App Malrechnen

Einleitung

Für das Erlernen eines umfassenden Operationsverständnisses ist die flexible Verbindung entsprechender Darstellungen eine zentrale Fähigkeit, dessen praktische Umsetzung (nicht nur motorisch) herausfordernd sein kann. Besonders Kindern mit dem Förderschwerpunkt Geistige Entwicklung wird das Erlernen eines umfassenden und verständnisorientierten Operationsverständnisses häufig nicht zugetraut. Die Multiplikation ist eine grundlegende mathematische Operation, die auch in alltäglichen Kontexten eine wichtige Rolle spielt, z.B. beim Umgang mit Geld oder bei der Essensplanung. Folglich ist das Erlernen und Nutzbarmachen der Multiplikation für Kinder im Förderschwerpunkt Geistige Entwicklung grundsätzlich anzustreben. Die hier vorgestellten Aktivtäten sind praktisch erprobt. Sie zeigen ohne Anspruch auf Vollständigkeit ausgewählte Möglichkeiten, mit der App „Malrechnen“ als Hilfsmittel zu arbeiten und betonen das verständnisorientierte Üben durch die anschauliche Darstellung der Verbindungen zwischen den unterschiedlichen multiplikativen Darstellungsformen.

Für die Erprobung wurde ein möglicher Leitfaden entwickelt, mit Hilfe dessen die Reihe durchgeführt wurde. Sie finden ihn sowie weitere Hinweise für eine mögliche Umsetzung am Ende von diesem Text.

In der folgenden Darstellung wird ein Einblick gegeben, wie die App "Malrechnen" im Rahmen des Gemeinsamen Lernens zum verständigen Üben flexibler Verbindungen zwischen unterschiedlichen multiplikativen Darstellungen auch mit Kindern mit dem Förderschwerpunkt Geistige Entwicklung sinnvoll eingesetzt werden kann.

Ayla (6. Jahrgang) und Anna (9. Jahrgang) haben den sonderpädagogischen Unterstützungsbedarf Geistige Entwicklung. Die beiden Mädchen besuchen seit der 5. Klasse eine Hauptschule des Gemeinsamen Lernens und kennen sich gut, denn im Rahmen von jahrgangsübergreifenden Förderstunden werden sie immer wieder gemeinsam unterrichtet.

Ayla kennt die Darstellung von Malaufgaben als Punktefelder, kann diese aber nicht sicher auf andere Darstellungen übertragen. Sie rechnet mit Unterstützung von Material und ihrer Schulbegleitung im Zahlenraum bis 100 Additions- und Subtraktionsaufgaben. Ayla kennt das Malzeichen und kann erste Aufgaben des kleinen 1x1 lösen.

Anna rechnet im Zahlenraum bis 20 meist sicher, wobei sie Additions- und Subtraktionsaufgaben mit Unterstützung von Material und einer Schulbegleitung lösen kann. Beim Abzählen größerer Mengen unterlaufen ihr immer wieder Fehler. Bisher hat sie keine Malaufgaben bearbeitet.

In der folgenden Videoszene lernen die beiden Mädchen die App „Malrechnen“ kennen. Sie bearbeiten einen ersten Arbeitsauftrag und erkunden die Möglichkeit, ein bestimmtes Punktefeld in der App einzustellen.

 

Im Folgenden werden Einsatzmöglichkeiten der App „Malrechnen“ in Partner- und Einzelarbeit vorgestellt. Die Aufgabenformate sind an einer inklusiven Klasse orientiert, besonders aber an Kindern mit dem sonderpädagogischen Unterstützungsbedarf Geistige Entwicklung.

Die App bietet unterschiedliche Darstellungsformen für multiplikative Aufgaben an. Den Kern bildet ein Hunderterpunktefeld gekoppelt mit der entsprechenden Multiplikationsaufgabe. Zusätzlich können unterschiedliche Darstellungen der Multiplikationsaufgabe eingeblendet werden. Mögliche Darstellungen sind eine Zahlenlinie, eine Additionsaufgabe (fortgesetzte Addition), eine Divisionsaufgabe sowie eine Multiplikationstabelle. Alle Darstellungen passen sich der vom Kind oder der Lehrkraft eingestellten Multiplikationsaufgabe an, sodass die unterschiedlichen Darstellungen einer Aufgabe verglichen und genutzt werden können. Wenn Sie die grundlegenden Funktionen der App genauer kennenlernen möchten, können Sie hier ein Einführungsvideo anschauen.

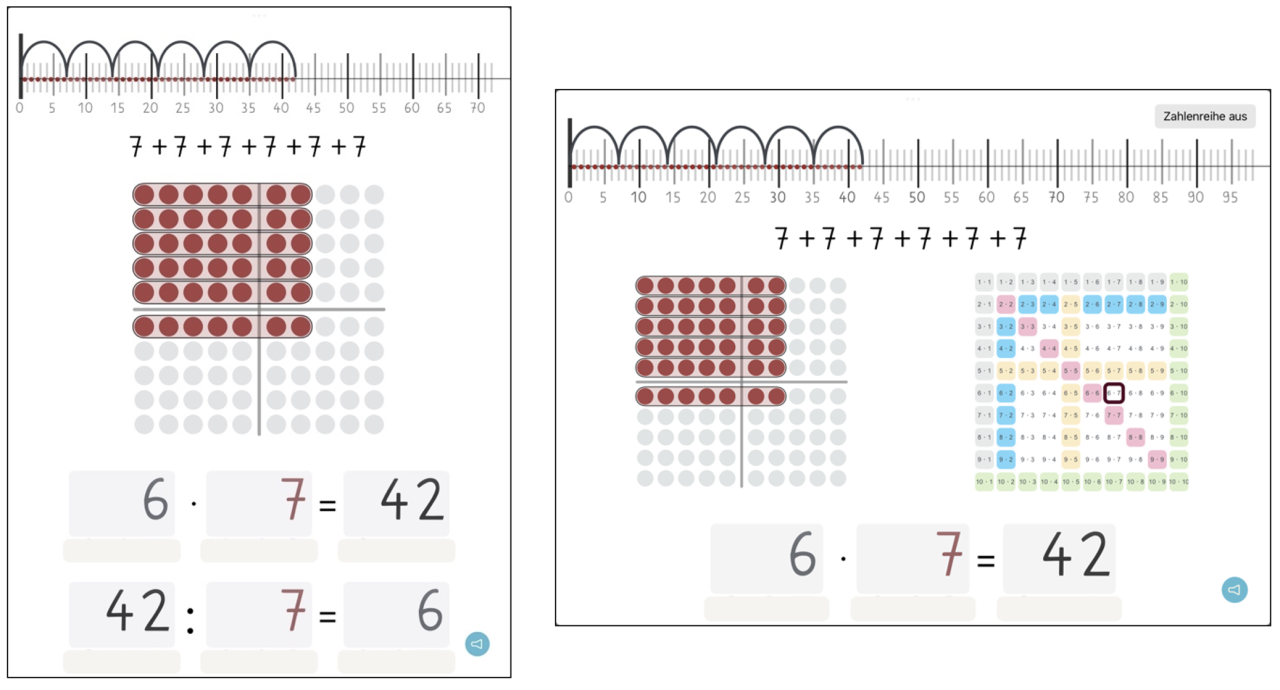
Abbildung 1: Screenshots der App Malrechnen mit aktivierten Zusätzen

Die App „Malrechnen“ stellt den Kindern keine Aufgaben. Die zu lösenden Aufgaben werden von der Lehrkraft oder dem Kind eingebracht. Die App dient als Unterstützung und Anschauungsmittel bei deren Bearbeitung. Neben dem Vorteil, dass das Erstellen von Punktefeldern sehr schnell und komfortabel möglich ist, ist ein weitaus größerer Vorteil, dass bestimmte multiplikative Zusammenhänge durch die Synchronität der Darstellungen in der App sehr gut verdeutlicht und schnell sichtbar werden können.

Unterschiedliche Einsatzmöglichkeiten sowie passende Aufgabenkarten, die in Kombination mit der App eingesetzt wurden, werden im Weiteren genauer vorgestellt sowie bereitgestellt und deren Einsatz wird mit kurzen Videoausschnitten verdeutlicht.

Vorüberlegungen zum Erlernen multiplikativer Strukturen im Förderschwerpunkt Geistige Entwicklung

Der Förderschwerpunkt Geistige Entwicklung zeichnet sich durch eine besonders hohe Heterogenität der Schülerschaft aus (weiterführende Informationen über den Förderschwerpunkt Geistige Entwicklung können hier nachgelesen werden). Die App „Malrechnen“ kann sowohl für die Erarbeitung der Multiplikation genutzt werden als auch für die Vertiefung, wenn schon erste Kenntnisse über die Multiplikation vorhanden sind.

Wie zu Beginn jeder neuen Reihe sollten in einem ersten Schritt die Vorkenntnisse der Kinder überprüft werden. Für die vorliegende Einheit stellt sich (nicht nur, aber besonders) für Kinder, die im Bildungsgang Geistige Entwicklung unterrichtet werden, die diagnostisch wichtige Frage, inwiefern die Kinder in der Lage sind, multiplikative Strukturen oder Ansätze davon kognitiv zu erfassen. Durch die große Heterogenität des Förderschwerpunkts kann es sein, dass manche Kinder (noch) nicht in der Lage sind, sich mit multiplikativen Strukturen und Vorstellungen auseinanderzusetzen, während andere ein operatives Verständnis zeigen. So ist im konkreten Fall zu prüfen, für welche Kinder die Erarbeitung der Multiplikation zu komplex ist und welche Kinder an einer (ggf. vereinfachten) Lernstandserhebung mit der Klasse teilnehmen können (z.B. von Mathe sicher können).

Besteht jedoch Unsicherheit, ob und inwiefern die Kinder in der Lage sind, eine Lernstanderhebung selbstständig zu bearbeiten, empfiehlt es sich, die Vorkenntnisse der Kinder in einer Kleingruppe oder wenn möglich sogar in einem Diagnosegespräch in einer Eins-zu-Eins-Situation zu erheben (nähere Informationen zu Diagnosegesprächen finden Sie hier). Inhalt des Gesprächs können Beschreibungen von Punktefeldern und multiplikativen Abbildungen, Additionsaufgaben (am besten Verdopplung oder auch schon fortgesetzte Addition) sowie die Frage nach passenden Aufgaben zu multiplikativen Abbildungen sein.

Die Kinder können ihrem individuellen Kenntnisstand entsprechend in die Arbeit eingebunden werden. Dabei ist zu beachten, dass weder die App „Malrechnen“ noch die entwickelten Materialien als selbsterklärend zu sehen sind. Deren Einsatz sollte von einer Lehrkraft eingeführt und begleitet werden, und zwar bei Kindern mit und ohne festgestelltem sonderpädagogischen Förderbedarf (weitere Informationen zur Einführung und zum Einsatz von mathematischen Anschauungs- und Darstellungsmitteln finden sich hier).

Um einige erprobte Möglichkeiten der konkreten Arbeit mit der App „Malrechnen“ zu demonstrieren, sind die im Folgenden dargestellten Aktivitäten mit vier Kindern mit dem Förderschwerpunkt Geistige Entwicklung in begleiteter Partnerarbeit an einer Hauptschule durchgeführt worden. Die dabei entstandenen Videosequenzen veranschaulichen die praktische Arbeit mit der App.

Vorüberlegungen zum Einsatz der Sprache beim Mathematiklernen im Förderschwerpunkt Geistige Entwicklung

Unterschiedliche empirische Studien zeigen einen starken statistischen Zusammenhang zwischen sprachlicher Kompetenz und Mathematikleistungen, sodass fachbezogene Sprachförderung mittlerweile fester Bestandteil der Lehrpläne geworden ist (vgl. u.a. Prediger 2019). Bei Menschen im Förderschwerpunkt Geistige Entwicklung gelten „solche Fähigkeiten, die zum Intelligenzniveau beitragen, wie Kognition, Sprache, motorische und soziale Fähigkeiten“ (Fornefeld 2020, S. 65), als besonders beeinträchtigt. Folglich besteht im Mathematikunterricht mit Kindern im Förderschwerpunkt Geistige Entwicklung fast immer ein erhöhter Bedarf an Sprachförderung und ggf. an sprachlicher Unterstützung. In welchem Umfang und in welcher Form die sprachliche Unterstützung sinnvoll erfolgen kann, muss jeweils im individuellen Fall entschieden werden.

Für die Kinder in der vorliegenden Einheit hat sich eine (laminierte) schriftliche Vorlage  im DIN A4-Format mit Satzbeispielen als gute Ergänzung zum verbalen Vorbild der Lehrkraft erwiesen.

Das Erlernen multiplikativer Strukturen

„Das Wort multiplizieren kommt aus dem Lateinischen. Es bedeutet ‚vervielfachen‘“ (Erichson 2008, S. 223) und kann als Vereinigung gleichgroßer Mengen verstanden werden (vgl. Transchel 2020). Die Multiplikation steht in enger Verbindung zur Addition als Vereinigung von Mengen und gilt als „eine verkürzte Addition immer derselben Zahl“ (Erichson 2008, S. 223). Die Vereinigung gleichgroßer Mengen kann auf drei tragfähige Vorstellungen aufgebaut werden, von denen zwei hier im Fokus stehen: zeitlich-sukzessiv und räumlich-simultan (die kombinatorische Vorstellung ist mit der App "Malrechnen" nicht zu bearbeiten und wird deswegen hier nicht näher erläutert, nähere Informationen dazu finden sich hier). In der zeitlich-sukzessiven Vorstellung werden gleichgroße Mengen nacheinander miteinander verbunden (eine Beispielhandlung für die Aufgabe 4•5 könnte sein: Ich gehe viermal in den Keller und hole jeweils 5 Flaschen). Bei der räumlich-simultanen Vorstellung können räumlich angeordnete Objekte multiplikativ beschrieben werden (z.B. in einer Getränkekiste: vier Reihen mit jeweils fünf Flaschen in jeder Reihe).

In der App „Malrechnen“ liegt der Schwerpunkt durch die Fokussierung auf das Punktefeld auf der räumlich-simultanen Vorstellung (wobei auch die zeitlich-sukzessive Vorstellung durch die Zahlenstrahldarstellung thematisiert werden kann). Mit der App können Verbindungen zwischen der Punktefelddarstellung, der Zahlenstrahldarstellung, der Darstellung einer Multiplikationstabelle, einer passenden sprachlichen Darstellung zum Punktefeld sowie der formalen Darstellung von Multiplikations-, Additions- und Divisionsaufgaben hergestellt werden. Auf diese Weise können multiplikative Vorstellungen sowohl neu aufgebaut als auch vertieft werden.

Die Fähigkeit zur flexiblen Verbindung der genannten Darstellungen ist grundlegend für das multiplikative Verständnis (nähere Information zum Operationsverständnis Multiplikation finden sich z.B. hier). Sie wird im Weiteren intensiv behandelt. Wenn die Kinder die Verbindungen zwischen den verschiedenen Darstellungen verstanden haben, können diese anhand der App gut geübt und gefestigt werden.

Verbindungen unterschiedlicher multiplikativer Darstellungen

Die Fähigkeit, unterschiedliche Darstellungen zu einer Rechenoperation miteinander in Verbindung bringen und zwischen ihnen flexibel wechseln zu können, ist grundlegend für ein umfassenden Operationsverständnis. Jede Darstellung hat ihre Besonderheiten und betont unterschiedliche Aspekte der Multiplikation. Bei den vorgestellten Aktivitäten werden die vier Darstellungen Punktefeld, sprachliche Darstellung, Additions- und Multiplikationsaufgabe erarbeitet und miteinander in Verbindung gebracht.

Multiplikative Punktefelder bestehen aus Punkten (z.B. dargestellt als Plättchen), die in Reihen und Spalten angeordnet sind, wobei in jeder Reihe jeweils die gleiche Menge an Punkten dargestellt ist. Gleiches gilt für die Spalten. Somit wird die multiplikative Struktur übersichtlich räumlich dargestellt und auf einen Blick wahrnehmbar. Punktefelder betonen entsprechend die räumlich-simultane Vorstellung der Multiplikation.

Sprachliche Darstellungen können mündlich oder schriftlich erfolgen. Eine eindeutige sprachliche Darstellung des multiplikativen Punktefeldes benennt z.B. die Anzahl der Reihen mit der Anzahl der Punkte in jeder Reihe: „X Reihen mit X Punkten in jeder Reihe.“ Die App „Malrechnen“ bietet als Sprachausgabe eine Kurzfassung an: „X Reihen mit X Plättchen“, die bei entsprechender Aktivierung jedes neu eingestellte Punktefeld beschreibt.

Multiplikative Punktefelder können sowohl über die sprachliche Darstellung als auch über eine Additions- und/oder eine Multiplikationsaufgabe eindeutig beschrieben werden.

Bei der passenden Additionsaufgabe handelt es sich um eine Additionsaufgabe im Sinne der fortgesetzten Addition, wobei die Anzahl der Reihen durch die Anzahl der Summanden beschrieben wird und die Anzahl der Punkte in jeder Reihe durch den Zahlenwert der Summanden. Die Summe ist die Gesamtanzahl aller dargestellten Punkte im Punktefeld. 

Bei der passenden Multiplikationsaufgabe wird die Anzahl der Reihen durch den 1. Faktor beschrieben und die Anzahl der Punkte in jeder Reihe durch den 2. Faktor. Das Produkt ist die Gesamtanzahl aller dargestellten Punkte im Punktefeld. Setzt man beide Aufgabenformate in Verbindung, so beschreibt der 1. Faktor der Multiplikationsaufgabe die Anzahl der Summanden der fortgesetzten Addition (und damit die Anzahl der Reihen im Punktefeld) und der 2. Faktor der Multiplikationsaufgabe den Zahlenwert der einzelnen Summanden in der fortgesetzten Addition (und so die Anzahl der Punkte in jeder Reihe).

Alle Darstellungsverbindungen der App noch einmal im Überblick:

• Punktefeld als räumlich-simultane Darstellung mit sprachlicher Darstellung („X Reihen mit X Punkten in jeder Reihe“)
• Anzahl der Reihen im Punktefeld = X Reihen = 1. Faktor in der Multiplikationsaufgabe = Anzahl der Summanden in der fortgesetzten Addition
• Anzahl der Punkte pro Reihe im Punktefeld = X Punkte in jeder Reihe = 2. Faktor in der Multiplikationsaufgabe = Zahlenwert der einzelnen Summanden in der fortgesetzten Addition

Für ein tragfähiges multiplikatives Verständnis ist von zentraler Bedeutung, dass Punktefelder, Additionsaufgaben und Multiplikationsaufgaben miteinander verknüpft und sprachlich korrekt beschrieben werden. Im Weiteren werden unterschiedliche Aktivitäten zur Übung dieser Verbindungen vorgeschlagen, die auch mit Kindern mit dem Unterstützungsbedarf Geistige Entwicklung erprobt wurden.

Mögliche Aktivitäten zu Darstellungsverbindungen

1. Partnerarbeit (mit 2 iPads): Kind 1 stellt ein Punktefeld auf seinem iPad ein und beschreibt dieses Punktefeld für Kind 2 entsprechend des eingeführten Sprachmusters („X Reihen mit X Plättchen in jeder Reihe“); Kind 2 stellt das Punktefeld auf seinem iPad entsprechend ein; die Kinder vergleichen und korrigieren ggf. das Ergebnis.

In der folgenden Videoszene „Punktefelder einstellen und beschreiben“ arbeiten Ayla (6. Jahrgang) und Eleni (7. Jahrgang) gemeinsam an der vorgestellten Aktivität. Beide werden im Gemeinsamen Lernen einer Hauptschule im Bildungsgang Geistige Entwicklung unterrichtet und treffen sich im Rahmen von jahrgangsübergreifenden Förderstunden wöchentlich. Beide Kinder haben Malaufgaben in Verbindung mit Punktefeldern bereits in der Grundschule kennengelernt. Die Verbindung zwischen der verbalen Darstellung und einem Punktefeld wurde im Vorfeld zu der Videoszene erarbeitet. Die Videoszene zeigt einen kurzen Einblick in die oben beschriebene Übungseinheit.

Mögliche Beobachtungsschwerpunkte für die folgende Videosequenz:

1. Inwiefern trägt die Aufgabe zum Verständnisaufbau der Multiplikation bei Ayla und Eleni bei?
2. Welche Rolle übernimmt die Lehrkraft in dieser Videoszene?
3. Inwiefern könnten Sie sich diese Aufgabe auch ohne Anleitung durch eine Lehrkraft vorstellen?

 

Lesen Sie hier mögliche Beobachtungen zur Videosequenz

Mögliche Beobachtungen zu Schwerpunkt 1. (Verständnisaufbau): Eleni scheint die Verbindung zwischen der verbalen Darstellung und dem Punktefeld bereits gut zu gelingen. Für sie stellt die Aufgabe eine Möglichkeit der Automatisierung dar. Ayla zeigt dagegen noch Unsicherheiten bei der Bestimmung der Anzahl der Reihen. Elenis Sicherheit kann Ayla hier in mehreren Durchgängen helfen, selbst mehr Sicherheit mit der Verbindung von verbaler Darstellung und Punktefeld zu bekommen.    

Mögliche Beobachtungen zu Schwerpunkt 2. (Rolle der Lehrkraft): Die Lehrkraft übernimmt hier die Moderation der Aufgabe sowie das Anbieten von Hilfsmitteln (hier das Bereitstellen und Einsetzen des Sprachspeichers für die Verbalisierung des Aufbaus der Punktefelder). Sie dient als Verbindungsglied zwischen den beiden Mädchen.

Möglichkeiten der Umsetzung zu Schwerpunkt 3. (Partnerarbeit ohne Lehrkraft): Sollte diese Aufgabe ohne kontinuierliche Unterstützung der Lehrkraft durchgeführt werden, ist es wichtig, dass der Ablauf für die Kinder gut nachvollziehbar, ggf. bereits eingeübt ist. Durch die Arbeit ohne Lehrkraft wäre es denkbar, dass die beiden Mädchen mehr direkt miteinander ins Gespräch kommen und so der mathematische Austausch intensiver gelingen kann. Als Hilfestellungen sollten neben dem Sprachspeicher auch im Vorfeld Vorgehensweisen besprochen werden, was die Kinder zu tun haben, wenn die Punktefelder nicht zusammenpassen oder wenn sie gemeinsam nicht weiterkommen.

---

2. Partnerarbeit (mit einem iPad): Kind 1 füllt die sprachliche Darstellung der Punktefeldbeschreibung auf einer Aufgabenkarte, auf der nur das Punktefeld vorgegeben ist (vgl. Abb.2), aus und beschreibt damit Kind 2 das Punktefeld auf der Karte, sodass Kind 2 das Punktefeld in der App einstellen kann. Das Punktefeld auf der Karte und das in der App können zur Kontrolle verglichen werden.

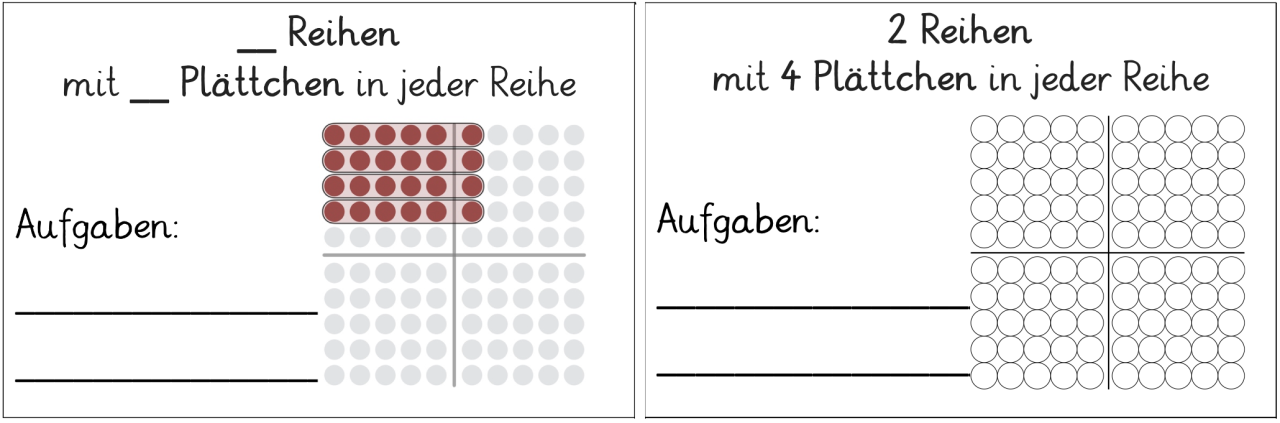
Abbildung 2: Aufgabenkarten, nur Punktefeld vorgegeben bzw. nur sprachliche Darstellung

In der nun folgenden Videoszene „Punktefeld und Sprache“ arbeiten Ayla (6. Jahrgang) und Anna (9. Jahrgang) gemeinsam an der 2. Aktivität in Partnerarbeit. Die beiden Mädchen mit dem Förderschwerpunkt Geistige Entwicklung werden im Gemeinsamen Lernen unterrichtet und treffen sich immer wieder im Rahmen von jahrgangsübergreifenden Förderstunden. Beide haben direkt vor der Szene eine Karte mit einem vorgegebenen Punktefeld (s. Abb. 2) bekommen und die verbale Darstellung selbstständig ausgefüllt.

Mögliche Beobachtungsschwerpunkte für die folgende Videosequenz:

1. Inwiefern trägt die Aufgabe zum Verständnisaufbau der Multiplikation bei Ayla und Anna bei?
2. Welche Rolle übernimmt die Lehrkraft in dieser Videoszene?
3. Inwiefern könnten Sie sich diese Aufgabe auch ohne Anleitung durch eine Lehrkraft vorstellen?

 

Punktefeld und Sprache

Lesen Sie hier mögliche Beobachtungen zur Videosequenz

Mögliche Beobachtungen zu Schwerpunkt 1. (Verständnisaufbau): Im Rahmen der Videoszene ist kein direkter Verständnisaufbau bei Ayla und Anna zu beobachten. Es geht vorrangig um das Festigen und Automatisieren des bereits Verstandenen. Konkret wird hier die Verbindung zwischen Punktefeld und verbaler Darstellung multiplikativer Aufgaben in Partnerarbeit geübt.

Mögliche Beobachtungen zu Schwerpunkt 2. (Lehrerrolle): Die Lehrkraft übernimmt hier die Rolle der Moderatorin, indem sie strukturierende Fragen an die Kinder stellt bzw. strukturierende Aufforderungen ausspricht (z.B.: „Beschreibe du mal das Punktefeld, damit Anna es einstellen kann.“). Zudem erinnert sie Ayla an den Einsatz des Sprachspeichers und begleitet sie so bei der verbalen Darstellung.

Mögliche Beobachtungen zu Schwerpunkt 3. (Partnerarbeit ohne Lehrkraft): Da die Aufgabe sich durch eine feste und sich wiederholende Struktur auszeichnet, eignet sie sich grundsätzlich gut als unbegleitete Partnerarbeit. Dennoch ist es wichtig, dass der Ablauf für die Kinder im Vorfeld ausgiebig trainiert und ggf. geklärt wird, welches Kind die einzuhaltende Struktur im Blick behält, sodass die Lehrkraft nur noch sporadisch gebraucht wird. Als Hilfestellungen sollten neben dem Sprachspeicher auch im Vorfeld Vorgehensweisen besprochen werden, was die Kinder zu tun haben, wenn die Punktefelder nicht zusammenpassen.

---

3. Einzelarbeit: Das Kind stellt anhand von Aufgabenkarten, auf denen jeweils eine sprachliche Darstellung der Beschreibung eines Punktefeldes vorgegeben ist (vgl. Abb. 2), das entsprechende Punktefeld in der App ein und kontrolliert die Lösung anhand der Sprachausgabe in der App oder anhand der Lösung auf der Rückseite der Karte.

4. Einzelarbeit: Das Kind füllt Aufgabenkarten aus, auf denen jeweils nur das Punktefeld vorgegeben ist (vgl. Abb. 2) und kontrolliert die Lösung mit der App oder anhand der Lösung auf der Rückseite der Karte.

5. Partnerarbeit (mit 2 iPads): Beide Kinder füllen auf einer leeren Aufgabenkarte eine (ggf. von der Lehrkraft vorgegebene) Darstellung aus (z.B. nur die Anzahl der Reihen und der Plättchen oben auf der Karte oder nur die Malaufgabe) und ergänzen die komplette Lösung auf der Rückseite. Dann tauschen die Kinder die Aufgabenkarten, um die entsprechenden Punktefelder in der App einzustellen und die Karten auszufüllen. Je nach Leistungsstand können die Aufgabenanzeigen in der App aus- oder angeschaltet (Plusaufgabe) bzw. sichtbar oder abgedeckt (Malaufgabe) sein.

Variante: Es werden leere Karten ohne Lösungsrückseite genutzt. Jedes Kind füllt jeweils eine Karte, wie oben beschrieben, aus, tauscht diese mit dem Partnerkind und beide Kinder bearbeiten die erhaltene Karte. Die App (mit eingeschalteter Plus- und sichtbarer Malaufgabe) dient als Lösungskontrolle, in dem das entsprechende Punktefeld eingetragen wird und dadurch alle weiteren Elemente kontrolliert werden können.

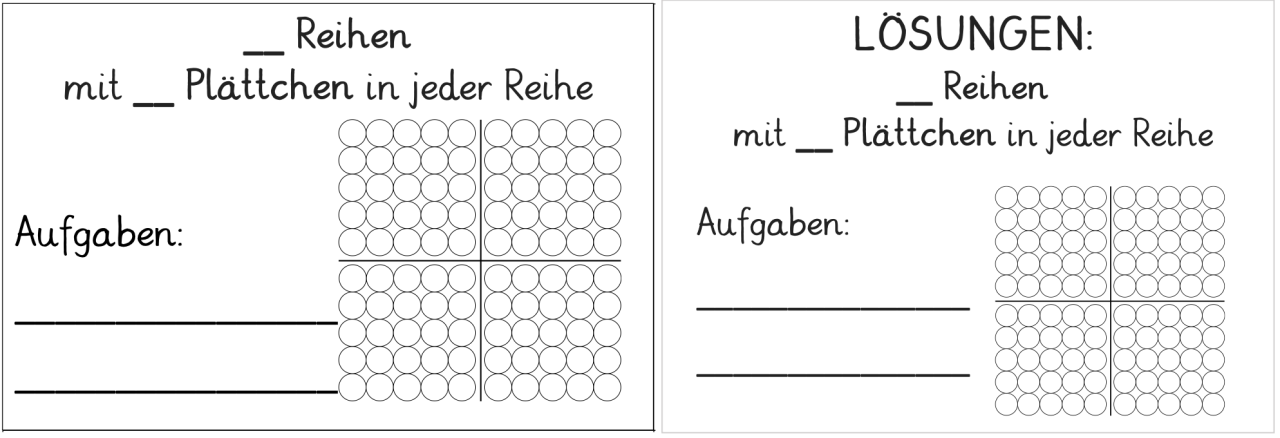
Abbildung 3: leere Aufgabenkarte ohne Vorgaben (Vorder- und Rückseite)

 

6. Partnerarbeit (mit einem iPad): Kind 1 erstellt in der App ein Punktefeld (mit zugedeckter Malaufgabe) und zeigt es Kind 2. Kind 2 nennt die passende Malaufgabe und die Kinder kontrollieren durch Aufdecken der Malaufgabe, ob Kind 2 die passende Malaufgabe genannt hat.

Für die umgekehrte Richtung: Kind 1 nennt eine Malaufgabe; Kind 2 stellt das entsprechende Punktefeld in der App (mit zugedeckter Malaufgabe) ein. Durch Aufdecken der Malaufgabe können die Kinder kontrollieren, ob Kind 2 das passende Punktefeld eingestellt hat.

7. Einzelarbeit: das Kind stellt anhand von Aufgabenkarten, auf denen jeweils eine Malaufgabe vorgegeben ist, das entsprechende Punktefeld in der App (mit abgedeckter Malaufgabe) ein und kontrolliert die Lösung durch Aufdecken der Malaufgabe in der App oder anhand der Lösung auf der Rückseite der Karte. Für die umgekehrte Richtung: Aufgabenkarten mit vorgegebenen Punktefeldern nutzen (vgl. Abb. 2) und die Malaufgabe aufschreiben.

Für die umgekehrte Richtung: Aufgabenkarten mit vorgegebenen Punktefeldern nutzen (vgl. Abb. 2) und die Malaufgabe aufschreiben.

Variante: Das Kind füllt die gesamte Aufgabenkarte aus und kontrolliert mit Hilfe der App, ob die Lösungen richtig sind.

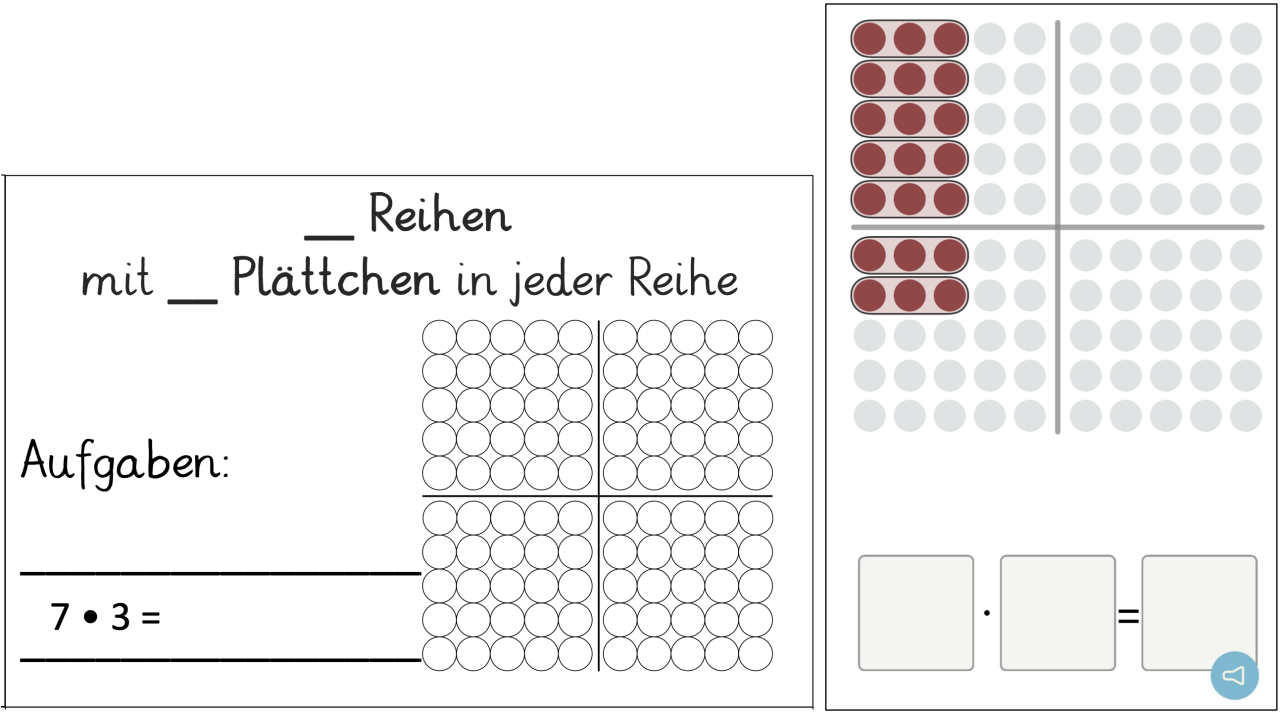
Abbildung 4: Aufgabenkarte, nur Multiplikationsaufgabe vorgegeben und App-Ansicht mit abgedeckter Multiplikationsaufgabe

8. Partnerarbeit (mit einem iPad und Aufgabenkarten): Kind 1 liest die Malaufgabe auf der Aufgabenkarte vor; Kind 2 stellt das passende Punktefeld in der App (mit zugedeckter Malaufgabe) ein und kontrolliert dieses dann anhand der App oder der Lösungen auf der Rückseite der Aufgabenkarte.

9. Partnerarbeit (mit einem iPad): Kind 1 erstellt in der App ein Punktefeld (mit zugedeckter Malaufgabe, aber eingeschalteter Plusaufgabe) und beschreibt es Kind 2; Kind 2 nennt die passende Plusaufgabe; Kind 1 kontrolliert anhand der App, ob Kind 2 die passende Plusaufgabe genannt hat.

Für die umgekehrte Richtung: Partnerarbeit (mit 2 iPads): Kind 1 nennt eine Plusaufgabe; Kind 2 stellt das entsprechende Punktefeld in der App (mit zugedeckter Malaufgabe und eingeschalteter Plusaufgabe) ein.

10. Einzelarbeit: das Kind stellt anhand von Aufgabenkarten, auf denen jeweils eine Plusaufgabe vorgegeben ist, das entsprechende Punktefeld in der App (mit abgedeckter Malaufgabe und eingeschalteter Plusaufgabe) ein und kontrolliert die Lösung anhand der Lösung auf der Rückseite der Karte.

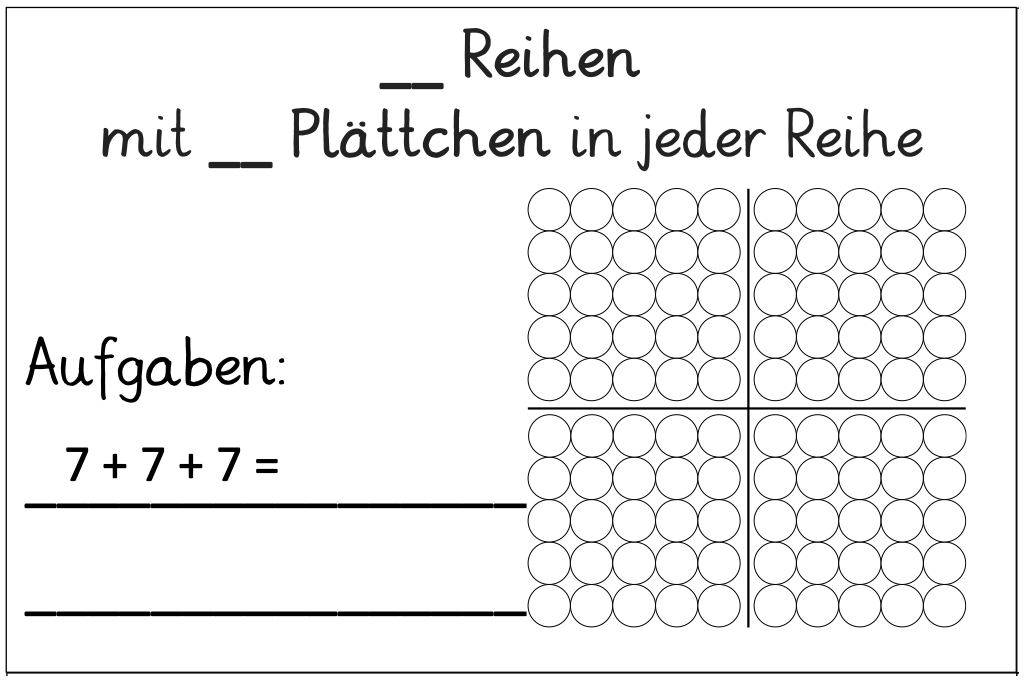
Abbildung 5: : Aufgabenkarte, nur Additionsaufgabe vorgegeben 

 

11. Partnerarbeit (mit einem iPad): Kind 1 erstellt in der App ein selbsterdachtes Punktefeld (mit zugedeckter Malaufgabe, aber eingeschalteter Plusaufgabe) und nennt die Plusaufgabe; Kind 2 nennt die passende Malaufgabe; Kind 1 kontrolliert anhand der App, ob Kind 2 die passende Malaufgabe genannt hat.

Für die umgekehrte Richtung: Kind 1 stellt ein Punktefeld in der App ein und nennt die Malaufgabe; Kind 2 nennt die passende Plusaufgabe; Kind 1 kontrolliert anhand der App, ob Kind 2 die passende Plusaufgabe genannt hat.

12. Partnerarbeit (mit einem iPad und Aufgabenkarten): Kind 1 liest die Malaufgabe auf der Aufgabenkarte vor (vgl. Abb. 4), Kind 2 nennt die passende Plusaufgabe und stellt das entsprechende Punktefeld in der App ein (ggf. in Absprache mit Kind 1); Kind 2 kontrolliert anhand der App, ob es die passende Plusaufgabe genannt hat.

Für die umgekehrte Richtung: Kind 1 liest die Plusaufgabe auf der Aufgabenkarte vor (vgl. Abb. 5), Kind 2 nennt die passende Malaufgabe und stellt das entsprechende Punktefeld in der App ein (ggf. in Absprache mit Kind 1); Kind 2 kontrolliert anhand der App, ob es die passende Malaufgabe genannt hat.

In der folgenden Videosequenz arbeiten Nina und Eleni (beide 7. Jahrgang) miteinander. Beide werden im Gemeinsamen Lernen einer Hauptschule im Bildungsgang Geistige Entwicklung in derselben Klasse unterrichtet und sehen sich entsprechend täglich. Gezeigt wird die 4. gemeinsame Einheit der Multiplikationsförderung, sodass alle bisher beschriebenen multiplikativen Verbindungen (sprachliche Darstellung, Punktefeld, Mal- und Plusaufgabe) thematisiert werden. Den Ausgangspunkt für die Aktivität bildet die Malaufgabe auf einer ansonsten unausgefüllten Aufgabenkarte (vgl. Abb. 4).

Mögliche Beobachtungsschwerpunkte für die folgende Videosequenz:

1. Welche Schwierigkeit beim Operationsverständnis kann bei Eleni beobachtet werden und mit welcher Strategie wurde diese gelöst?
2. Welche Rolle spielt die Lehrkraft in der Szene?
3. Inwiefern können Sie sich eine Umsetzung der Aufgabe ohne kontinuierliche Begleitung durch die Lehrkraft vorstellen?

 

Punktefeld und Plusaufgabe zur Malaufgabe

Lesen Sie hier mögliche Beobachtungen zur Videosequenz

Mögliche Beobachtungen zu Schwerpunkt 1 (Schwierigkeit beim Operationsverständnis): Eleni zeigt zu Beginn der Szene, dass sie Punktefeld, verbale Darstellung und Malaufgabe miteinander richtig verbinden kann. Dennoch hat sie auch nach mehreren Übungseinheiten noch die Tendenz 2 • 10 = 2 + 10 zu denken. Um diese Fehlvorstellung aufzulösen, kann die Vorstellung der „Pakete“ bei der Multiplikation als Vereinigung gleichgroßer Mengen (vgl. Transchel 2020) genutzt werden. Die gleichgroßen Mengen werden als „Pakete“ beschrieben, in denen jeweils gleichviele Punkte drin sind. Die App unterstützt diese Vorstellung durch das Umkreisen der „Pakete“. Somit kommen in dieser Aufgabe zwei Pakete mit jeweils 10 Punkten vor, also zwei Zehner oder 10 + 10.

Mögliche Beobachtungen zu Schwerpunkt 2 (Lehrerrolle): Die Lehrerin übernimmt auch hier die Aufgabe der Moderatorin und achtet besonders darauf, dass die Aufgabenverteilung eingehalten wird und Nina nichts für Eleni vorwegnimmt. Zudem leitet sie die Strategie der „Pakete“ an, um Eleni an diese Strategie zu erinnern.

Mögliche Beobachtungen zu Schwerpunkt 3 (Partnerarbeit ohne Lehrkraft): Diese Aufgabe eignet sich grundsätzlich gut als Partnerarbeit zur Übung aller hier behandelten multiplikativen Verbindungen. Wenn eines der Kinder die multiplikativen Verbindungen schon wesentlich besser beherrscht als das andere (wie in dieser Szene Nina), könnte dieses Kind die Moderatorenrolle übernehmen bzw. die klare Aufforderung bekommen, dem anderen Kind nichts vorweg zu nehmen, sondern die Übung zu „leiten“.

Die Videoszene zeigt, dass das Beherrschen bestimmter multiplikativer Verbindungen nicht unbedingt dazu führt, dass ein vollständiges multiplikatives Operationsverständnis vorliegt. Eleni zeigt auch nach mehreren Übungseinheiten noch die Tendenz 2 x 10 = 2 + 10 zu denken. In diesem Sinne ist neben der Verbindung unterschiedlicher Darstellungen auch die Klärung des multiplikativen Verständnisses gegenüber dem additiven Verständnis notwendig.

Unterscheidung und Verbindung von Addition und Multiplikation

Im Verlauf der praktischen Förderung ist immer wieder aufgefallen, dass bei der Verbindung von Addition und Multiplikation die folgende Fehlvorstellung auftrat: 6 • 5 = 6 + 5. Dies wurde zum Anlass genommen, das additive Verständnis (etwas zu einer Menge hinzufügen, zwei oder mehrere Mengen zusammenfügen) dem multiplikativen Verständnis (gleichgroße Mengen mehrmals nehmen, eine Menge vervielfachen) gegenüber zu stellen und anhand des Punktefeldes und der passenden Aufgaben voneinander abzugrenzen.

Die folgenden Videosequenz zeigt genau dieses Fehlverständnis und einen Korrekturversuch. Wie in der vorherigen Videosequenz, arbeiten auch hier Eleni und Nina zusammen, beide werden im Gemeinsamen Lernen im Bildungsgang Geistige Entwicklung im 7. Jahrgang unterrichtet. Eleni zeigt die beschriebene Fehlvorstellung. Um diese aufzubrechen, wird das Punktefeld in der App „Malrechnen“ als Anschauungsmittel sowie als sprachliche Begleitung der Begriff der „Pakete“ („immer 6 in einem Paket“) genutzt. Diese „Punkte-Pakete“ werden im Punktefeld der App eingekreist und farblich hinterlegt (vgl. Abb. 4).

Mögliche Beobachtungsschwerpunkte für die folgende Videosequenz:

1. Inwiefern kann Eleni die neue Vorstellung der fortgesetzten Addition verstehen und annehmen?
2. Was genau konnte ihr aus Ihrer Sicht hier helfen, was hat sie nicht weitergebracht?
3. Inwiefern können Sie sich eine Umsetzung der Aufgabe ohne kontinuierliche Begleitung durch die Lehrkraft vorstellen?

 

Mal- und Plusaufgaben zum Punktefeld

Lesen Sie hier mögliche Beobachtungen zur Videosequenz

Mögliche Beobachtungen zu Schwerpunkt 1 (Verständnisaufbau): Eleni kann zu Beginn der Szene nicht erklären was es bedeutet, Mal oder Plus zu rechnen bzw. was der Unterschied zwischen den beiden Operationen ist. Im Laufe der Szene setzt sie sich mit der Vorstellung der Multiplikation als Addition gleichgroßer „Pakete“ auseinander und kann am Ende die richtige Plusaufgabe formulieren. Dies gelingt ihr an dieser Stelle jedoch nur mit Unterstützung durch Nina und die Lehrkraft, die ihr die Sechser-Pakete in der App anzeigen und sie somit auffordern, diese zusammenzurechnen.

Mögliche Beobachtungen zu Schwerpunkt 2 (Unterstützung beim Verständnis): Eleni fiel es schwer, die Plusaufgabe ohne direkten Bezug zu dem Punktefeld bzw. zu den einzelnen Reihen (hier benannt als Pakete) im Punktefeld zu bilden. Für sie war die Abbildung auf dem Punktefeld und die Möglichkeit, die zusammenzurechnenden Pakete direkt zu zeigen, ein gutes Hilfsmittel.

Mögliche Beobachtungen zu Schwerpunkt 3 (Partnerarbeit ohne Lehrkraft): Da es in dieser Szene um den Verständnisaufbau des Operationsverständnisses von Addition und Multiplikation geht, sowie die Abgrenzung zwischen diesen beiden Operationen, ist die Lehrkraft an dieser Stelle nur schwer zu ersetzen. Wenn dieses Verständnis gesicherter ist, kann die grundsätzliche Aufgabe, die Karte auszufüllen und dann der Partnerin das Punktefeld anhand einer anderen Darstellung zu beschreiben, damit diese es dann auf dem iPad in der App einstellt, wiederum sehr gut auch ohne Lehrkraft möglich.

Verdeutlichung des Kommutativgesetzes (Vertauschungsgesetz)

Die Multiplikation ist eine kommutative Operation, d.h. dass sich das Ergebnis nicht verändert, wenn die beiden Faktoren vertauscht werden: 3 • 4 = 12 = 4 • 3.

Anhand der Punktefelddarstellung lässt sich die Vertauschung von Faktoren gut nachvollziehbar darstellen und überprüfen, denn die App „Malrechnen“ macht es möglich, mit einem Knopfdruck die automatische Darstellung der Tauschaufgabe einzuschalten und so Ausgangs- und Tauschaufgabe anschaulich zu betrachten.

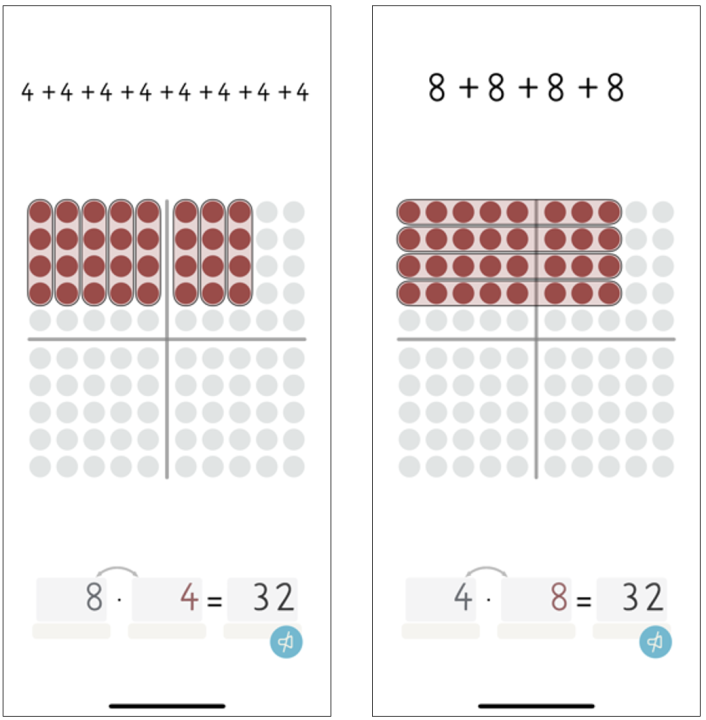
Abbildung 6: App-Ansicht einer Tauschaufgabe und der entsprechenden Bündelung der Plättchen ohne Veränderung der Gesamtanzahl

Mögliche Aktivitäten zur Übung des Kommutativgesetzes

1. Partnerarbeit (mit 2 iPads): Beide Kinder bekommen eine Aufgabenkarte (Aufgabenkarten "Mal und Plus als Tauschaufgabe 6 und 7") mit der jeweiligen Tauschaufgabe des anderen Kindes und stellen dazu entsprechend das Punktefeld in der App ein. Die beiden Punktefelder werden mit der Ausgangsaufgabe: „Was fällt euch auf?“ verglichen.

2. Partnerarbeit (mit 1 iPad): Kind 1 ohne iPad nennt eine Malaufgabe, Kind 2 mit iPad stellt das entsprechende Punktefeld in der App ein und nennt die Tauschaufgabe bzw. nutzt ggf. die App, um die Tauschaufgabe zu ermitteln. Die App kann sowohl die Hilfestellung geben als auch als Kontrolle genutzt werden.

Eine mögliche Umsetzung der Aktivitäten

Grundsätzlich sind die vorgestellten Aktivitäten als Anregungen gedacht, die App Malrechnen im Mathematikunterricht einzubinden. Dabei können alle Kinder mit der App arbeiten oder sie kann ein Zusatzangebot für ausgewählte Kinder darstellen, die besonders von der Anschaulichkeit und der leichten Bedienung der App profitieren.

Für die gezeigte Partnerarbeit mit den Mädchen mit Unterstützungsbedarf Geistige Entwicklung wurde im Vorfeld ein Leitfaden entwickelt, den sie zusammen mit den Aufgabenkarten und anderen Materialien hier finden. Dieser beinhaltet neben konkreten Formulierungen und Fragen, jeweils eine Aufzählung des eingesetzten Materials, einen didaktischen Kommentar mit formulierten Zielen sowie die vorgenommenen Einstellungen der App Malrechnen.

Inhaltliche Ziele sind zu Beginn die Wiederholung der Darstellungsverbindungen sowie die Einführung der sprachlichen Darstellung und der App Malrechnen (im Leitfaden: „Vorarbeit 1 und 2“). Des Weiteren standen Übungen der unterschiedlichen Darstellung mit Hilfe der App im Vordergrund (im Leitfaden: 1.–4.). Für einige Kinder bot sich noch eine zusätzliche Einheit zum Zusammenhang von Tauschaufgaben an (im Leitfaden: „Zusatz“).

Je nach Fähigkeiten der Kinder sollte individuell auf deren Fortschritte eingegangen werden, z.B. könnten bei gutem Verständnis zwei Einheiten zu einer Einheit zusammengefasst werden oder bei Bedarf auch Wiederholungen von Einheiten eingebaut werden.

Im Gemeinsamen Lernen könnten die ersten Einheiten zu einer zusammengefasst werden, so dass die Kinder der Klasse die sprachlichen Strukturen kennenlernen, die App zu zweit erkunden und dann am Ende der Stunde die Funktionen der App zusammentragen und die sprachlichen Darstellungen entsprechend auf die App übertragen. Der Einsatz der Aufgabenkarten und der unterschiedlichen Übungen multiplikativer Strukturen sollte dann individuell für die Kinder der Klasse anhand der zu übenden Darstellungsverbindungen ausgewählt werden.

Die Aktivitäten in Kombination mit den exemplarischen Videosequenzen können Sie vielleicht unterstützen, Kinder mit dem Unterstützungsbedarf Geistige Entwicklung verständnisorientiert an das Thema Multiplikation heranzuführen, weitere sinnvolle Einsatzmöglichkeiten für die App „Malrechnen“ zu finden und das Format „Aufgabenkarte“ als zusätzliches Arbeitsmittel zu nutzen.

Zitierte Literatur

• Erichson, C. (2008). Von Null bis Zett. Mathematik nachschlagen. Lernbuchverlag.
• Fornefeld, B. (2020). Grundwissen Geistigbehindertenpädagogik. 6. Auflage. Ernst Reinhardt.
• Prediger, S. (2019). Mathematische und sprachliche Lernschwierigkeiten. Empirische Befunde und Förderansätze am Beispiel des Multiplikationskonzepts. Lernen und Lernstörungen, 8(4), 247–260. https://doi.org/10.1024/2235-0977/a000268.
• Transchel, S. (2020). Gemeinsames Lernen multiplikativer Zusammenhänge. Struktur-fokussierende Deutungen bei Kindern mit Schwierigkeiten im Fach Mathematik. Springer Spektrum