Im Förderschwerpunkt Geistige Entwicklung werden Schülerinnen und Schüler mit ganz unterschiedlichen kognitiven Fähigkeiten und Entwicklungsständen unterrichtet – die Spannweite „reicht von Schülerinnen und Schülern, die ein Kompetenzniveau an der Grenze zum zieldifferenten Bildungsgang Lernen aufzeigen, bis hin zu Schülerinnen und Schülern, die einen erhöhten oder komplexen Unterstützungsbedarf aufweisen“ (MSB_RL 2022, 8). Das (Mathematik-)lernen dieser Schülerinnen und Schüler ist nicht nur beeinflusst durch die intellektuelle Beeinträchtigung, sondern oft auch durch Schwierigkeiten in den Bereichen Sprache und Arbeitsgedächtnis oder durch eine Sinnesbeeinträchtigung, die häufig mit der intellektuellen Beeinträchtigung einhergeht. Bei der Planung und Durchführung von Mathematikunterricht mit dieser Gruppe von Lernenden müssen also nicht nur Leistungsstände und Vorwissen in Mathematik berücksichtigt werden, sondern auch die allgemeinen Lernvoraussetzungen. Die Falldarstellungen von Mark, Marie und Felix im Einstieg verdeutlichen die Unterschiede zwischen den Lernenden. Manche Lernende müssen in Mathematik noch Kompetenzen erwerben, die Kinder in der Regel vor Schuleintritt erwerben, während andere Lernende an Inhalten der Grundschulmathematik arbeiten.
Die individuellen Lernvoraussetzungen und großen Unterschiede zwischen den Lernenden mit und ohne intellektuelle Beeinträchtigung bringen Herausforderungen für das gemeinsame Lernen mit sich. Das Anpassen von Aufgaben ist kaum ausreichend und das Lernen an einem gemeinsamen Gegenstand scheint unmöglich, vor allem wenn es Lernende in der Klasse gibt, die noch an mathematischen Basiskompetenzen arbeiten, deren Verbindung mit den Inhalten der jeweiligen Schulstufe sich kaum erkennen lässt.
Wie sollen alle Kinder an gemeinsamen Inhalten lernen, wenn sie so unterschiedliche Lernvoraussetzungen, Bedürfnisse und Ziele haben? Der Mathematikunterricht kann immer wieder alltagsnahe und lebenspraktisch bedeutsame Themen aufgreifen, die den Zugang zu mathematischen Begriffen und Verfahren für alle Lernenden erleichtern. Den einzelnen Lernenden kann er nur durch qualitative Differenzierung annähernd gerecht werden, also durch unterschiedliche Ziele und Aufgaben auf unterschiedlichen Schwierigkeitsstufen und mit individuell angepassten Aktivitäten. Für diese Art von Differenzierung ist Wissen über die mathematischen Basiskompetenzen und deren Bedeutung für das weitere Mathematiklernen notwendig.
Lebenspraktischer Bezug
Das Aufgreifen und Thematisieren von mathematischen Aspekten in Alltagssituationen kann alle Lernenden dabei unterstützen, mathematische Begriffe und Kompetenzen im lebenspraktischen Bereich anzuwenden. Dies gilt insbesondere für Lernende mit Unterstützungsbedarf im Schwerpunkt Geistige Entwicklung.
Mit lebenspraktischem Bezug ist nicht gemeint, dass der Mathematikunterricht durchgehend und ausschließlich lebenspraktisch orientiert sein soll, sondern dass immer wieder alltagsbedeutsame Themen und Aktivitäten aufgegriffen und genutzt werden, auch in Situationen außerhalb des Mathematikunterrichts. Im Schulalltag können z.B. Zahlen und Mengen bestimmt und verglichen werden. Mögliche Aktivitäten sind das Suchen von Zahlen während eines Klassenausflugs, das Abzählen der Kinder zu Beginn der Sportstunde oder das Ausführen additiver Handlungen beim Zusammenstellen einer Bücherkiste.
Wenn im Mathematikunterricht der Bezug zu lebenspraktischen Bereichen hergestellt wird, muss wohl überlegt sein, ob dadurch die Einsicht in den mathematischen Inhalt gefördert wird, z.B. beim Einbeziehen operativer Alltagshandlungen zur Erarbeitung des Operationsverständnisses. Denn das Einbetten von Aufgaben in Sachsituation kann zu einem Lernhindernis werden, wenn das Verstehen der Situation aus dem lebenspraktischen Bereich bereits herausfordernd ist oder nicht der Lebenswelt der Lernenden entspricht.
Der Einsatz von Geld hat zwar einen großen lebenspraktischen Bezug und ist für die Lernenden motivierend, aber Geld ist eine sehr abstrakte Größe. Für den Umgang mit Geld sowie mit anderen Größen ist das kardinale Verständnis von Zahlen eine Voraussetzung (Scherer & Moser Opitz, 2010).
Mathematische Basiskompetenzen
Die mathematischen Basiskompetenzen sind die Grundlage für das Mathematiklernen, weil sie für den Aufbau von Zahlvorstellungen und für den Erwerb weiterer mathematischer Kompetenzen notwendig sind (Kuratli, Moser Opitz & Schnepel, 2020). Insbesondere dem Verbinden von Zahlen mit Mengen kommt eine hohe Bedeutung zu. Die Lernenden müssen erkennen, dass zu jeder Zahl eine bestimmte Menge gehört und zu jeder Menge ein bestimmtes Zahlwort. Diese Einsicht wird auch als kardinale Zahlvorstellung oder präzise Mengenvorstellung bezeichnet.
Während ein Großteil der Kinder ohne intellektuelle Beeinträchtigung bereits im ersten Schuljahr zu dieser Einsicht gelangt, stellt sie für Lernende im Förderschwerpunkt Geistige Entwicklung häufig eine Herausforderung dar. Sie brauchen mehr Zeit und ein großes Übungsangebot, bei dem sie immer wieder Mengen zählen, legen, zeichnen und ordnen. Diese Aktivitäten tragen dazu bei, kardinale Zahlvorstellungen aufzubauen. Diese sind genauso wie die Einsicht in das Teil-Ganze-Konzept (Inhalte – Zahlvorstellungen – Zahlen zerlegen) eine wichtige Voraussetzung um Additionssaufgaben zu verstehen und zu lösen (Krajewski & Ennemoser, 2013). Ohne diese Voraussetzungen werden Rechenaufgaben häufig durch Zählen in Einerschritten gelöst. Die Kinder haben dabei nur Einerschritte „im Blick“ und nicht die Summanden (Häsel-Weide, Nührenbörger, Moser Opitz & Wittich, 2019).
Jedoch sehen Lernende mit intellektueller Beeinträchtigung, insbesondere im inklusiven Unterricht, wie die anderen Kinder Rechnungen lösen und sie sind stolz, wenn ihnen das auch gelingt. Deshalb kann das Legen von Additionsaufgaben mit Material genutzt werden, um einerseits weiter an der Zahlvorstellung zu arbeiten und andererseits erste Erfahrungen mit Additionsaufgaben zu machen. Entscheidend dabei ist der Fokus, den die Lehrkraft setzt. Beim Legen von Additionsaufgaben bzw. Mengen am Zwanzigerfeld sollen Schwerpunkte gesetzt werden, die dem Aufbau kardinaler Zahlvorstellungen und der Einsicht in das Teil-Ganze-Konzept dienen und sich mit Rechnungen verbinden lassen, und nicht das Lösen der Aufgaben. Folgende Aktivitäten sind geeignet:
-
Kardinale Zahlvorstellung: Die Teilmengen so legen, dass sie sich „auf einen Blick“ erkennen lassen. Eine Menge legen. Was passiert, wenn ich ein Plättchen dazu lege? Wie heißt die Zahl dann?
-
Einsicht in das Teil-Ganze-Konzept: Aufgaben, die immer 10 ergeben, z.B. 2 rote und 8 blaue Plättchen. Was passiert, wenn ich ein blaues Plättchen auf die rote Seite drehe? Wie viele rote und blaue Plättchen sind es dann? Wir viele Plättchen sind es zusammen? Es sind immer 10, weil ich kein Plättchen dazu oder weggenommen habe.
-
Vorstellungen aufbauen: Lege 5 Plättchen ins Zwanzigerfeld. Jetzt schließe die Augen. Stell dir vor ich lege ein Plättchen dazu. Wie viele sind es? Ein Plättchen dazu legen. Mach die Augen auf und überprüfe ob das Bild aus deinem Kopf mit dem Zwanzigerfeld übereinstimmt.
-
Operationsverständnis: zu einer Menge eine weitere Menge hinzufügen, zwei Teilmengen vereinigen.
Konkrete Ideen wie bei der halbschriftlichen Addition Lernende mit intellektueller Beeinträchtigung miteinbezogen werden können und das Lernen an einem gemeinsamen Gegenstand gestaltet werden kann, finden sich in dem unten aufgeführten Beispiel.
Möchten Sie sich eingehender mit mathematischen Basiskompetenzen befassen? Didaktische Analysen, Ideen zur Förderung und exemplarische Materialien für den Unterricht finden Sie auf der Seite von Mathe inklusiv mit PIKAS in der Rubrik Inhalte - Zahlvorstellungen.
Differenzierung: Gemeinsamer Inhalt und Förderung der Basiskompetenzen
In gutem Mathematikunterricht können alle Lernenden individualisiert, differenziert und gemeinsam lernen. Sie können Inhalte ganzheitlich in fachlich sinnvollen Zusammenhängen strukturiert auf ihrem jeweiligen Niveau bearbeiten.
Auch wenn die Kinder auf ihrem individuellen Niveau lernen, ist für den kommunikativen Austausch und für soziale Interaktionen ein gemeinsamer Lerninhalt nötig. Deshalb soll die Förderung der Lernenden im Förderschwerpunkt Geistige Entwicklung am Klassenunterricht anknüpfen, so dass die Grundlagen für einen thematischen Austausch und für Kooperation geschaffen werden und gleichzeitig soll der Schwerpunkt ihrer Förderung auf den Basiskompetenzen liegen. Das heißt also, dass der Inhalt im Schulbuch oder die Kompetenz im Lehrplan mit einer Basiskompetenz verbunden werden muss. Es müssen geeignete Anknüpfungspunkte gefunden werden und diese sind der gemeinsame Lerninhalt, an dem die Kinder aufgrund von Differenzierungsmaßnahmen ihrem Niveau entsprechend arbeiten können (Krähenmann, Labhart, Schnepel, Stöckli & Moser Opitz, 2015).
Um das gemeinsame Lernen zu ermöglichen, sind Unterrichtssequenzen notwendig, in denen sich die Lernenden über ihre Vorgehensweisen und ihren Wissensstand austauschen können. Besonders geeignet sind gemeinsame Einstiegs- und Reflexionsphasen. Zu Stundenbeginn kann ein spezifischer Lerninhalt mit den unterschiedlichen Erfahrungen der Lernenden verbunden werden. In Reflexionsphasen am Ende der Stunde können die Lernenden die Inhalte reflektieren, sich über neue Erkenntnisse und Fragen austauschen und Ideen und Gedanken verbalisieren und darstellen.
Individualisiertes Lernen ist in den Arbeitsphasen dazwischen möglich, in denen durch Differenzierung auf die individuellen Lernausgangslagen der Lernenden eingegangen wird. Damit die Kinder in dieser Phase möglichst selbständig arbeiten, sind klare Aufgabenstellungen in wiederkehrenden Formaten mit bekannten Materialien und Strukturen besonders geeignet. Nicht nur Lernende mit intellektueller Beeinträchtigung sind auf eine klare Strukturierung angewiesen. Selbständiges Arbeiten der Kinder ermöglicht der Lehrkraft in dieser Zeit einzelne Lernende individuell zu unterstützen, z.B. durch eine direkte Ansprache oder das Verbalisieren von Handlungsabläufen.
Differenzieren ist anspruchsvoll, bedarf der Übung und die Auswahl der Methoden, Aufgaben und Ziele muss von der Lehrkraft ständig reflektiert und adaptiert werden. Die folgenden Aspekte bieten Möglichkeiten zur Differenzierung:
-
Zahlenraum
-
Mit oder ohne Arbeitsmittel und Veranschaulichungen
-
Offene oder geschlossene Aufgaben
-
Aufgabenmenge: weniger Aufgaben, aber dafür fokussiert
-
Arbeitsform: allein, zu zweit, in Gruppen
In den Fällen von Mark, Marie und Felix (vgl. Einstieg) wären Anpassungen des Zahlenraums und der Einsatz von Arbeitsmittel nötig, aber nicht ausreichend. Für sie müssen individuelle Lernziele formuliert werden, die sich auf den gemeinsamen Lerninhalt beziehen und ihrer individuellen mathematischen Entwicklung entsprechen.
Auf der Seite von Mathe inklusiv mit PIKAS finden Sie in der Rubrik Inhalte unter dem Thema Differenzsensible Unterrichtsplanung als Grundlage des gemeinsamen Lernens weitere Beispiele und didaktischen Analysen.
Aber wie kann solch eine Differenzierung der Ziele und Unterrichtsinhalte konkret aussehen? Am Beispiel der halbschriftlichen Addition wird gezeigt, wie Lernziele formuliert und Unterrichtssequenzen gestaltet werden können, wenn Lernende wie Mark, Marie und Felix in der Klasse unterrichtet werden.
Beispiel: Halbschriftliche Addition
Ausgangspunkt: Mathematikbuch oder Lehrplan
Kompetenzerwartung am Ende der Klasse 4: Die Schülerinnen und Schüler lösen Aufgaben aller vier Grundrechenarten unter Ausnutzung von Rechengesetzen und Zerlegungsstrategien mündlich oder halbschriftlich. (Lehrplan Mathematik für die Grundschulen des Landes Nordrhein-Westfalen)
Beschreibung einer inklusiven Klasse: In der Klasse sind Kinder
-
mit tragfähigen Zahl- und Operationsvorstellungen im Zahlenraum bis 1000,
-
die zählend rechnen,
-
mit Zahlvorstellungen im Zahlenraum bis 100 (so wie Felix),
-
mit Zahl- und Operationsvorstellungen im Zahlenraum bis 20 (so wie Mark),
-
mit ersten Zahlvorstellungen bis 6 (so wie Marie).
Gemeinsame Lernziele: Welche mathematischen Kompetenzen sollen die Lernenden entwickeln?
Alle Schülerinnen und Schüler
-
festigen und erweitern ihre Zahlvorstellungen, indem sie Anzahlen und Zahlen verbinden,
-
vertiefen das Operationsverständnis, indem sie mental oder mit Arbeitsmaterial additive Handlungen durchführen.
Individuelle Lernziele: Welche mathematischen Kompetenzen sollen die Lernenden entwickeln?
(1) Lernende mit tragfähigen Zahl- und Operationsvorstellungen im Zahlenraum bis 1000
-
wenden eine halbschriftliche Rechenstrategie an, z.B. „Stellenwert extra“,
… indem sie Zahlen in die verschiedenen Einheiten (H, Z, E) zerlegen und gleiche Einheiten zuerst addieren und anschließend die Summen der Einheiten addieren.
-
wenden weitere halbschriftliche Rechenstrategien an,
… indem sie die Lösungswege anderer Kinder nachvollziehen und auf andere Aufgaben übertragen.
(2) Zählende Rechnerinnen und Rechner
-
vertiefen das Zahlverständnis (dezimale Struktur und Stellenwert),
… indem sie die Aufgaben mit Dienes-Material und Stellenwertkarten legen und Anzahlen „auf einen Blick“ erfassen.
-
lösen sich vom Zählen in Einerschritten,
… indem sie beim Addieren in Zehner- und Hunderterschritten zählen (123+50 → „Es kommen 5 Zehner dazu: 133, 143, 153, 163, 173“).
(3) Lernende mit Zahlvorstellungen im Zahlenraum bis 100
-
vertiefen das Zahlverständnis (dezimale Struktur und Stellenwert)
… indem sie Zahlen im Zahlenraum 100 mit Dienes-Material und Stellenwertkarten legen und Anzahlen „auf einen Blick“ erfassen.
-
festigen additive Grundvorstellungen,
… indem sie zu einer mit Material dargestellten Zahl zunächst Einer hinzufügen und danach zur gleichen Zahl die gleiche Menge Zehner hinzufügen (24+2, 24+20).
Felix
Wie Eingangs beschrieben ist das Ziel von Felix, dass er seine Stellenwertvorstellungen vertieft. Er kann Zahlen der Größe nach ordnen und stellengerecht schreiben. Ein langfristiges Ziel ist, dass er Additions- und Subtraktionsaufgaben ohne Material lösen kann. Dafür ist es wichtig, dass er mit dem Dienes-Material dargestellte Mengen «auf einen Blick» erfassen kann und weiß, wie sich die Zahlen verändern, wenn zur Menge Einer oder Zehner dazu gelegt werden.
Um selbständig arbeiten zu können, braucht er Visualisierungen von Handlungsabfolgen, regelmäßig eine individuelle Ansprache und Aufgaben, bei denen er nicht viel schreiben muss.
Individuelle Lernphase
Felix löst zuerst Aufgaben ohne Bündeln, dann Aufgaben mit Bündeln.
Bsp. für Aufgaben ohne Bündeln:
24+2, 24+20
56+3, 56+30
45+4, 45+40
Bsp. für Aufgaben mit Bündeln:
90+1, 90+10
49+2, 49+20
68+6, 68+60
Bei jeder Aufgabe führt Felix folgende Schritte aus, die mit Bildkarten visualisiert sind.
Lege:
Prüfe:
Schreibe/ zeichne das Ergebnis:

(4) Lernende mit Zahl- und Operationsvorstellungen im Zahlenraum bis 20
-
festigen das Anzahlkonzept,
… indem sie Anzahlen im Zahlenraum bis 20 strukturiert legen und diesen Zahlenkarten zuordnen.
-
festigen additive Grundvorstellungen,
… indem sie zu einer mit Material dargestellten Zahl zunächst Einer hinzufügen und danach zur gleichen Zahl die gleiche Menge Zehner hinzufügen (24+2, 24+20).
Mark
Mark rechnet im Zahlenraum bis 20 Additions- und Subtraktionsaufgaben mit Material. Sein Ziel ist der weitere Aufbau von tragfähigen Zahl- und Operationsvorstellungen. Langfristige Ziele sind, dass er die Struktur vom Zwanzigerfeld erkennt und nutzt, um Mengen auf einen Blick zu erfassen und dass er Einblicke in einen größeren Zahlenraum erhält.
Damit er bei Additionsaufgaben, die er im Zwanzigerfeld legt, nicht die Summanden und Summe jeweils abzählt, soll er «ähnliche» Aufgaben legen und vergleichen, bei denen er die Beziehungen zwischen Zahlen und Rechnungen entdecken kann.
Individuelle Lernphase
Arbeitsmaterial: Mark arbeitet meistens mit Wendeplättchen, die er auf das Zwanzigerfeld legt. Beim Dienes-Material fehlt ihm die Struktur. Er weiß nicht, wie er das Material vor sich auf dem Tisch anordnen soll, so dass er auf einen Blick die Anzahl erkennen kann. Deshalb arbeitet er weiterhin mit dem Zwanzigerfeld, auf das er Zehnerstreifen oder Wendeplättchen legt.
Repräsentationsebene: Wenn Mark die Rechnungen am Zwanzigerfeld legt, sieht er immer nur die aktuelle Rechnung vor sich und nicht die vorherige. Deshalb kann er keine Beziehungen zwischen den Aufgaben entdecken. Durch einen Wechsel von der enaktiven Ebene mit dem konkreten Material zur ikonischen Ebene mit Punktdarstellungen können die Aufgaben festgehalten und verglichen werden, so dass sie ihm das Entdecken von Zahlbeziehungen ermöglichen.
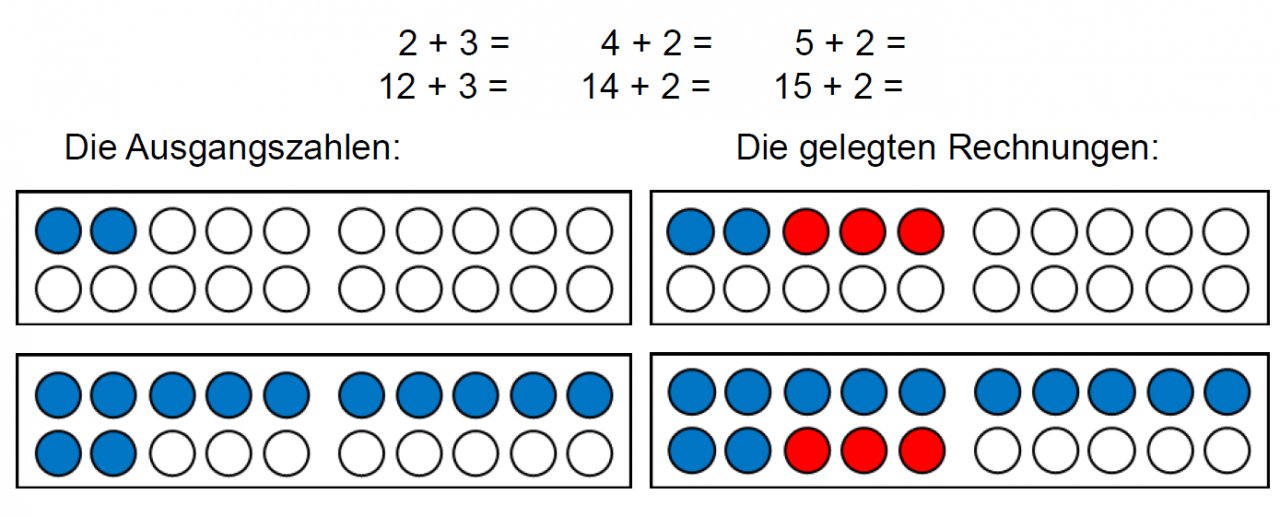
Zahlenraum: Mark ist schon in der 7. Klasse und arbeitet immer noch im Zahlenraum bis 20. Das Arbeiten in einem größeren Zahlenraum ist für ihn motivierend und kann zu neuen Einsichten führen. Möglich wären Aufgaben, bei denen immer 10 addiert werden, also immer ein Zehnerstreifen dazu gelegt wird: 2+10, 12+10, 22+10, …
Bei solchen Aufgaben erhält Mark die Möglichkeit, Muster bzw. Zahlbeziehungen zu entdecken, entweder selbständig oder durch gezieltes Nachfragen der Lehrkraft.
(5) Lernende mit Zahlvorstellungen bis 6
-
festigen das Anzahlkonzept,
… indem sie Anzahlen im Zahlenraum bis 10 abzählen und diesen Zahlenkarten zuordnen.
-
entwickeln Zahlvorstellungen,
… indem sie Einerwürfel, Zehnerstangen und Hunderterplatten unterscheiden.
Marie
Ein wichtiges Ziel von Marie ist die eindeutige Zuordnung von Zahlen und Mengen. Förderlich sind Aufgaben, bei denen sie Mengen zählen, legen oder ordnen muss (vgl. in der Rubrik Inhalte zum Thema Zahlvorstellungen das Zählen von Objekten).
Marie braucht zum Lernen konkretes Arbeitsmaterial, mit dem sie sich ausdauernd und konzentriert beschäftigen kann. Kurze überschaubare Lernsequenzen und viele Wiederholungen sind nötig, um neue Kompetenzen zu erwerben und zu festigen.
Individuelle Lernphase
Marie beteiligt sich beim Legen des Materials in der Gruppe der zählenden Rechnerinnen und Rechner. Sie verwaltet das Material und gibt die entsprechende Zahl Einerwürfel, Zehnerstangen und Hundertertafeln raus.
Die Zusammenarbeit mit anderen Kindern muss anfangs von der Lehrkraft begleitet werden.
Für die Reflexionsphase bereitet Marie das Material vor: Sie legt die Mengen, die auf einer Vorlage abgebildet sind, mit Material nach. Sie muss dabei Hunderterplatten, Zehnerstangen und Einerwürfel unterscheiden.
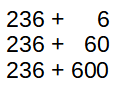

Nicht immer lassen sich in den Arbeitsphasen Möglichkeiten zur Zusammenarbeit mit anderen Kindern finden.
Mit Arbeitsmappen und Kistenaufgaben in Anlehnung an TEACCH kann Marie selbständig arbeiten (z.B. Solzbacher, 2011). Sie ordnet Mengenkarten den entsprechenden Zahlen zu oder bildet Mengen zu vorgegebenen Zahlen. Die Aufgaben haben immer eine ähnliche Struktur und deren Dauer entspricht ihrer Konzentrationsspanne.
Damit das selbständige Lernen gelingt, müssen die Aufgaben sorgfältig und mit sprachlicher Begleitung eingeführt werden. Auch wenn Marie eine Aufgabe beendet hat, ist es wichtig, mit ihr darüber zu sprechen. Sie kann z.B. aufgefordert werden die Zahlen vorzulesen oder, wenn die Zahlen der Reihe nach geordnet sind, kann der Bezug zwischen ordinalem und kardinalem Zahlaspekt thematisiert werden: Das ist die Zahlenreihe. Immer, wenn man eine Zahl weitergeht, ist es ein Punkt mehr.
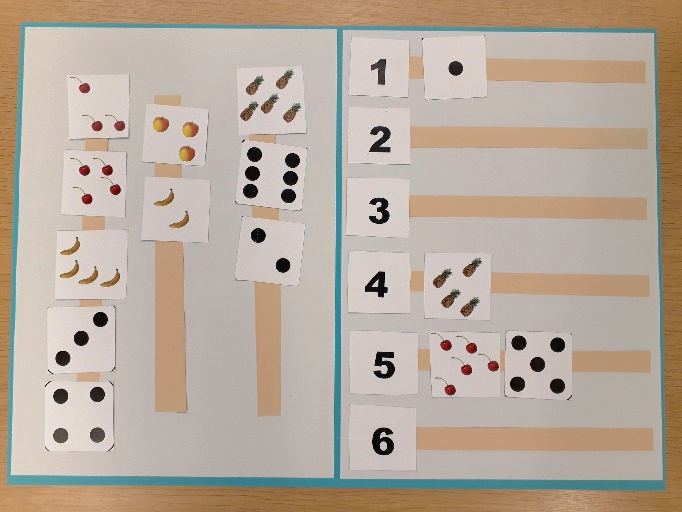
Arbeitsmappen nach TEACCH haben immer die gleiche Struktur. Die Karten von der linken Seite müssen auf die rechte Seite geheftet werden. Hier sollen die Karten mit Mengen der entsprechenden Zahl zugeordnet werden.
Gemeinsame Lernsequenzen
Einstiegsphase
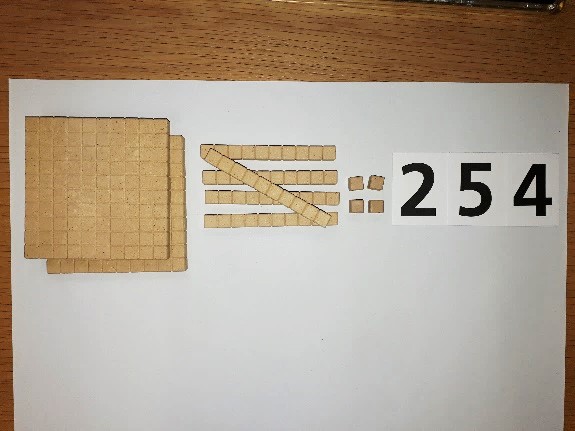
Im Kreis liegen das Dienes-Material, Stellenwertkarten und Karten mit Rechnungen (251+3, 251+30, 251+300).
„Wer kann diese Rechnung mit dem Dienes-Material legen? Wer legt sie mit den Stellenwertkarten?“
Karten mit Rechnungen an drei Kinder verteilen. Diese legen die drei Rechnungen mit dem Dienes-Material (siehe Abbildung).
Wer macht was?
Mark und Marie geben die benötigte Anzahl E, Z und H („Gib mir drei Einerwürfel“).
Drei andere Kinder (u.a. Felix) legen die entsprechenden Stellenwertkarten dazu.
Die anderen Kinder kontrollieren, ob alles stimmt und ob das Material so liegt, dass man ohne Abzählen erkennt, wie viel es ist.
Nachfragen: „Siehst du sofort, wie viele Einerwürfel es sind / wie viele Zehnerstangen es sind? Kannst du das Material so legen, dass du NICHT zählen musst?“



„Stimmt alles? Was fällt euch auf? Vergleicht die drei Aufgaben.“
-
Es ist immer 251.
-
Es kommen immer 3 dazu, hier 3 Einer, hier 3 Zehner, hier 3 Hunderter.
-
Es wird immer grösser / Es wird immer mehr, usw.
„Wie heißen die Ergebnisse der Rechnungen? Wer kann das Material so legen, dass man das Ergebnis sofort sieht?“ (Es sind verschiedene Anordnungen möglich.) Evtl. lautes Zählen in Zehner- und Hunderterschritten beim Dazulegen der Zehnerstangen/Hunderter: „251, 261, 271, 281“.


Reflexionsphase
Wer bringt sich wie in die Reflexionsphase ein?
-
Mark legt die Aufgaben 5+2 und 15+2 mit Punktestreifen und Plättchen.
-
Felix legt die Aufgaben 46+5 und 46+50 mit dem Dienes-Material.
-
Marie hat bereits die Aufgaben 236+6, 236+60, 236+600 mit Dienes-Material gelegt.



-
Andere Kinder legen die Zahlenkarten zu den Mengen und schreiben die Rechnungen dazu.
-
Die Aufgaben können auch gezeichnet werden. Weitere Anregungen finden sich in der Rubrik Inhalte beim Thema Stellenwertvorstellungen.
Bei jeder Aufgabe wird besprochen:
-
Was kommt dazu?
-
Wo verändert sich etwas bei der Rechnung?
-
Was verändert sich beim Material?
-
Muss etwas getauscht werden?
-
Wie heißt das Ergebnis?
Zahleiche weitere Möglichkeiten zur Gestaltung gemeinsamer Lernphasen werden in der Rubrik Leitideen unter Austausch anregen beschrieben und didaktisch kommentiert.
Wie können Reflexions-, Verbalisierungs- und Darstellungsprozesse angebahnt werden?
Die Schülerinnen und Schüler müssen gezielt angeleitet werden. Hilfreich ist das Anknüpfen an Aufgaben oder Produkten aus der individuellen Arbeitsphase und der Einbezug von konkreten Materialien. Die Lernenden können z.B. Ergebnisse präsentieren oder ihre Vorgehensweise mit Material zeigen. Den Visualisierungen kommt eine hohe Bedeutung zu, weil damit der Gesprächsgegenstand weniger abstrakt ist und auf Fragen der Lehrkraft durch Zeigen geantwortet werden kann. Die sprachliche Begleitung kann zunächst von der Lehrkraft oder anderen Kindern übernommen werden. Sie kann Handlungen beschreiben, Ergebnisse kommentieren und Impulse geben, indem sie z.B. folgende Fragen stellt:
-
Was fällt euch auf?
-
Vergleicht! Was ist gleich? Was ist anders?
-
Wer sieht etwas anderes?
-
Wie/Wo/Woran siehst du das?
-
Kannst du das mit Material zeigen?
-
Wer kann erklären, was Kind X meint?
-
Wie habt ihr das herausgefunden?
Die halbschriftliche Addition ist vor allem im 3. Schuljahr ein Thema, aber was mache ich mit Lernenden wie Mark, Marie und Felix, wenn ich eine 7. Klasse unterrichte?
Auch nach der Grundschule sind die Entwicklung von Zahl- und Operationsvorstellungen ein großes Thema, vor allem mit Bruch- und Dezimalzahlen. Lernende mit einer intellektuellen Beeinträchtigung können dann weiterhin am Aufbau von Zahl- und Operationsvorstellungen mit ganzen Zahlen arbeiten. Anknüpfungspunkte bei den Brüchen sind die Einsicht in Teil-Ganze-Beziehungen und das Zerlegen von Anzahlen.
Weitere Beispiele zur Differenzierung im inklusiven Mathematikunterricht finden sich in den Artikeln von Krähenmann, Labhart, Schnepel, Stöckli & Moser Opitz (2015) und Krähenmann & Schnepel (2016) zum Zählen und Bündeln und zum Verdoppeln.
Diese Seite wurde von Dr. Susanne Schnepel erstellt
und vom Team des Projekts „Mathe inklusiv mit PIKAS“ editiert.