Wenn Größen umgewandelt werden (sollen), werden die Maßeinheit und die Maßzahl in Relation zueinander so verändert, dass die Größe als solche konstant bleibt (z.B. wird 2 m in 200 cm oder 20 dm umgewandelt). Das Umwandeln von Größen hat für die Lernenden vor allem die Funktion, mit Größen zu rechnen und Größen handhabbar darzustellen (z.B. werden 2 dm in 200 mm umgewandelt, um 2 dm und 12 mm zu addieren – also 200 mm + 12 mm=212 mm – und daraufhin werden 212 mm in 2,12 dm umgewandelt).
Das Umwandeln von Längen erfolgt über das Umrechnen mit einer Umrechnungszahl und einer Umrechnungsoperation. Dabei handelt es sich bei der Umrechnungszahl um die Zahl (10, 100, 1000 usw.), mit der die Ausgangsmaßzahl multipliziert bzw. durch die sie dividiert werden muss, und bei der Umrechnungsoperation um die Multiplikation und die Division.
Gelingt es Schülerinnen und Schülern noch nicht, Längen auf diese Weise sicher und effizient umzurechnen, können sie Umwandlungen auch durch das Eintragen der Größenangaben in eine Stellenwerttafel, aus der dann die Ergebnismaßzahl abgelesen werden kann, durchführen.
Grundlagenkompetenzen für verständnisbasiertes Umrechnen
Für ein verständnisbasiertes Umrechnen sollten die Schülerinnen und Schüler sicher über mehrere Grundlagenkompetenzen verfügen, wie sie beispielsweise Lassnitzer und Gaidoschick sowie Schmassmann (2009, S. 180ff) beschreiben. Im Folgenden stellen wir vier zentrale Kompetenzen heraus:
-
Größenvorstellungen der Maßeinheiten
Die Schülerinnen und Schüler verfügen über gesicherte Größenvorstellungen der benutzten Maßeinheiten. Beispielsweise wissen die Lernenden, dass 1 cm so lang ist wie einer ihrer Finger breit und dass 50 cm einem kleinen Schritt oder der halben Höhe einer Schultafel (eine mögliche Größenvorstellung für die Länge 1 m) entsprechen. Mit dem Aktivieren von Größenvorstellungen können sich die Kinder noch vor dem eigentlichen Umrechnungsvorgang auf diesen Prozess einstellen und das Ergebnis in etwa abschätzen. Mit diesen Größenvorstellungen können sie zudem nach dem Umrechnen ihr Ergebnis auf Plausibilität überprüfen: „Unsere Tische sind ungefähr so tief wie ein kleiner Schritt lang ist. Das könnte stimmen!“
-
Inverse Beziehung zwischen Maßzahl und Maßeinheit
Das Verständnis für die inversen Beziehungen zwischen Maßzahl und Maßeinheit zielt auf die Erkenntnis, dass beim Umrechnen von einer größeren Maßeinheit in eine kleinere Einheit (bzw. umgekehrt) die Maßzahl relational zum Verkleinerungsfaktor größer (bzw. kleiner) werden muss (wird z. B. von m in cm umgerechnet, verhundertfacht sich die Maßzahl). Die Schülerinnen und Schüler wissen demnach, dass sie mehr kleinere Maßeinheiten aneinanderlegen müssen, um eine Länge auszulegen oder eben weniger größere Maßeinheiten (siehe die 2. grundlegende Idee des Messens (Verlinkung zu Messen)). Mit diesem Wissen können sie bereits vor der eigentlichen Umwandlung die Richtung bestimmen, in die sich die Maßzahl und die Maßeinheit verändern werden.
-
Beziehung zwischen den Maßeinheiten (dezimale Struktur)
Das Erkennen der Analogien zwischen dem dezimalen Stellenwertsystem und der dezimalen Struktur der Maßeinheiten (Ausnahme: Größe Zeit) erleichtert den Schülerinnen und Schülern sowohl das Verstehen der Beziehungen der Maßeinheiten zueinander als auch der dezimalen Zerleg- und Zusammensetzbarkeit der Längenmaßeinheiten. Sie können nicht nur im wortwörtlichen Sinn begreifen, dass 1 m genauso lang ist wie 10 dm und 100 cm und 1000 mm, sondern auch im übertragenen. Dies ist die Basis, um zu verstehen, wie sich die entsprechenden Umrechnungszahlen herleiten und nutzen lassen, um Größenangaben, die aus Maßzahl und -einheit bestehen, in andere Einheiten umzurechnen.
Ausgehend von der Basismaßeinheit Meter können auch die sinntragenden Vorsilben (aus dem Griechischen: Kilo für Tausend; aus dem Lateinischen: Dezi für Zehntel, Zenti für Hundertstel und Milli für Tausendstel) der einzelnen Maßeinheiten helfen, sich deren Beziehungen zueinander zu merken. Die Bedeutung dieser Vorsilben ist zudem in den Größenbereichen Länge, Volumen und Masse (Gewicht) einheitlich und kann sowohl von Lehrkräften als auch von Schülerinnen und Schülern genutzt werden, um diese Zusammenhänge zu verdeutlichen, zu verstehen und sich zu merken.
-
Multiplikation mit/Division durch 10, 100 und 1000
Die Schülerinnen und Schüler sollten für den Vorgang des Umrechnens das Bündeln und Entbündeln verstanden haben und durchführen können – auch über nicht direkt benachbarte Stellenwerte hinaus. Sie sollten wissen, dass 10 Einer gleich viel sind wie 1 Zehner, 10 Zehner so viel wie 1 Hunderter, 100 Einer so viel wie 1 Hunderter usw. Dieses Wissen und dieses Verständnis sollten dann auf den Bereich der Größen und auf die Beziehungen der Maßeinheiten zueinander übertragen werden können. Die Schülerinnen und Schüler wissen dann, dass 10 Zentimeter genauso lang sind wie 1 Dezimeter, 10 Dezimeter genauso so lang sind wie 1 Meter und 100 Zentimeter genauso lang sind wie 1 Meter. Mit diesem Wissen können sie die Umrechnungsoperationen verständnisbasiert und korrekt durchführen und sind nicht auf unverstandene Regeln wie „Nullen streichen oder anhängen“ oder „Komma verschieben“ angewiesen, die zu Fehlern führen können (z. B. 6,7 cm mal 100 = 6,700 cm).
Sind diese vier Grundkompetenzen für ein Umwandeln von Maßeinheiten nicht aufgebaut, besteht die Gefahr, dass die Schülerinnen und Schüler nicht verständig umrechnen können und stattdessen auf eine fehleranfällige, schematische Nutzung von Merksätzen, Anleitungen, Tabellen oder ähnlichem angewiesen sind. Mit geeigneten Aufgaben sollte die Lehrkraft deshalb erfassen, welche der oben genannten Grundlagenkompetenzen bei den Schülerinnen und Schülern verfügbar sind und worauf sie im Verlauf der Unterrichtsreihe gegebenenfalls noch einmal wiederholend oder sogar erarbeitend eingehen muss, damit das Umwandeln verständnisbasiert erarbeitet werden kann.
Die folgenden Aufgabenbeispiele bieten hierzu Hinweise. Möglicherweise müssen im Vorfeld Begriffe wie Meterstäbe und Dezimeterstäbe besprochen werden. Zudem sollte die Lehrkraft klären, ob alle Kinder die Maßeinheit Dezimeter im Unterricht thematisiert haben und über die notwendigen Rechenkompetenzen im Zahlenraum bis 10 000 verfügen.
 Abbildung 1: Standortbestimmung, Teil 1
Abbildung 1: Standortbestimmung, Teil 1
 Abbildung 2: Standortbestimmung, Teil 2
Abbildung 2: Standortbestimmung, Teil 2
Umwandeln von Längen mit der Stellenwerttafel
Die Stellenwerttafel verdeutlicht das Dezimalsystem. Kurz gesagt, jede Zahl besteht aus einer oder mehreren Ziffern, die aneinandergereiht den Wert der Zahl darstellen. Jede Ziffer repräsentiert dabei neben ihrem eigenen Wert auch den Wert der Stelle, an der sie innerhalb der Zahl steht. Der Wert der Stellen steigt von rechts nach links um den Faktor 10. Die Stellenwerttafel ist eine Tabelle, in der die Ziffern ihren entsprechenden Stellenwerten zugeordnet und so die Werte der einzelnen Ziffern einer Zahl dargestellt werden.
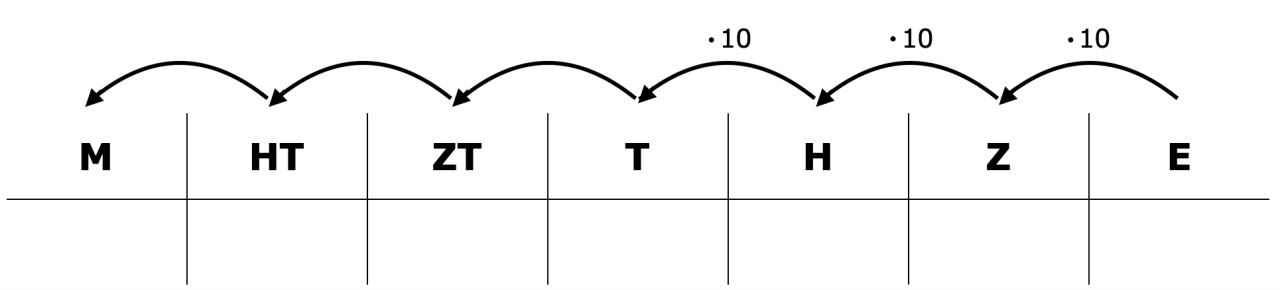 Abbildung 3: Stellenwerttafel
Abbildung 3: Stellenwerttafel
Bei den dezimalen Maßeinheiten (z. B. Längen, Masse, Volumen) werden analog zu den Stellen des Dezimalsystems ebenfalls 10 von einer Maßeinheit in eine nächstgrößere Maßeinheit sowie 1 von einer Maßeinheit in 10 nächstkleinere Maßeinheiten gewechselt.
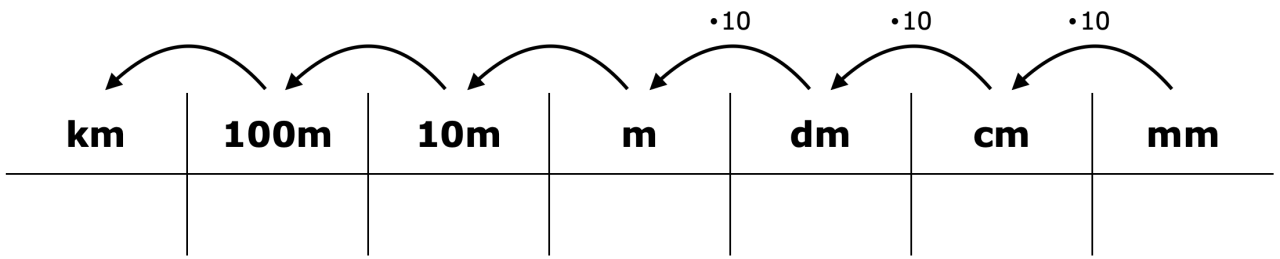 Abbildung 4: Längen-Stellenwerttafel
Abbildung 4: Längen-Stellenwerttafel
Stellenwerttafeln werden in der Primarstufe eingeführt und dort vor allem bei der Erschließung neuer Zahlenräume und zur Verdeutlichung des Stellenwertsystems eingesetzt. Im inhaltsbezogenen Kompetenzbereich Größen und Messen helfen Stellenwerttafeln den Kindern, die Beziehungen zwischen den unterschiedlichen dezimalen Maßeinheiten zu erkennen, eine Größenangaben von einer Einheit in eine andere umzurechnen und als Dezimalbruch zu schreiben. In der Sekundarstufe I kommen Stellenwerttafeln bei der Zahlraumerweiterung hin zu den positiven rationalen Zahlen und den darin enthaltenen Dezimalbrüchen sowie im Rahmen der Leitidee Messen zum Einsatz.
Umrechnen von Längen mit Umrechnungszahlen
Beim Umrechnen von Längen mit Umrechnungszahlen multiplizieren oder dividieren die Schülerinnen und Schüler die Maßzahlen der Ausgangslängen mit bzw. durch die entsprechenden Umrechnungszahlen. Grundlage für diese Umrechnungszahlen sind die Beziehungen zwischen den Maßeinheiten sowie deren Umkehrungen, von denen die am häufigsten benutzten zum sicheren Wissen vieler Kinder zählen. Diese Beziehungen können mit Karten wie den nachfolgenden symbolisch dargestellt werden, sollten aber auch immer wieder mit materialgebundenen Darstellungsformen (z. B. durch einen Holzstab, einen Papierstreifen oder einen Strich mit einer Länge von 1 m, auf dem 100 Abschnitte mit einer Länge von je 1 cm eingezeichnet sind) veranschaulicht werden.
 Abbildung 5: Karten mit Beziehungen zwischen Maßeinheiten (1)
Abbildung 5: Karten mit Beziehungen zwischen Maßeinheiten (1)
Andere Beziehungen zwischen Maßeinheiten sind häufig jedoch nicht verfügbar, da sie selten im Unterricht thematisiert wurden oder unbekannte oder „in Vergessenheit geratene“ Einheiten beinhalten.
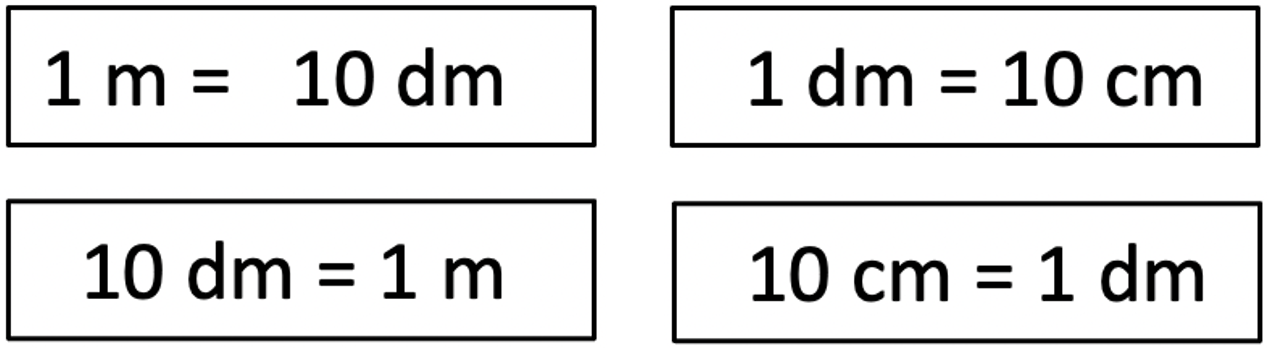 Abbildung 6: Karten mit Beziehungen zwischen Maßeinheiten (2)
Abbildung 6: Karten mit Beziehungen zwischen Maßeinheiten (2)
Aus diesen Beziehungen zwischen den Maßeinheiten ergeben sich die Umrechnungszahlen, die im folgenden Schaubild (vgl. Kupsch et al., 2018, S. 90) für die benachbarten Maßeinheiten dargestellt sind und mit denen die jeweiligen Maßzahlen multipliziert bzw. durch die sie dividiert werden. Hierbei gilt es, einen wichtigen Unterschied zur Längen-Stellenwerttafel zu beachten (und im Unterricht zu thematisieren): Während die Pfeilrichtung in der Längen-Stellenwerttafel die Veränderung der Maßeinheiten abbildet (z. B. 10 mal 1cm ist so lang wie 1dm.), verdeutlicht sie im Schaubild die inverse Veränderung der Maßzahl (z. B. Ich rechne eine Längenangabe in der Maßeinheit dm in die Maßeinheit cm um, indem ich die Maßzahl der dm-Länge mit 10 multipliziere.).
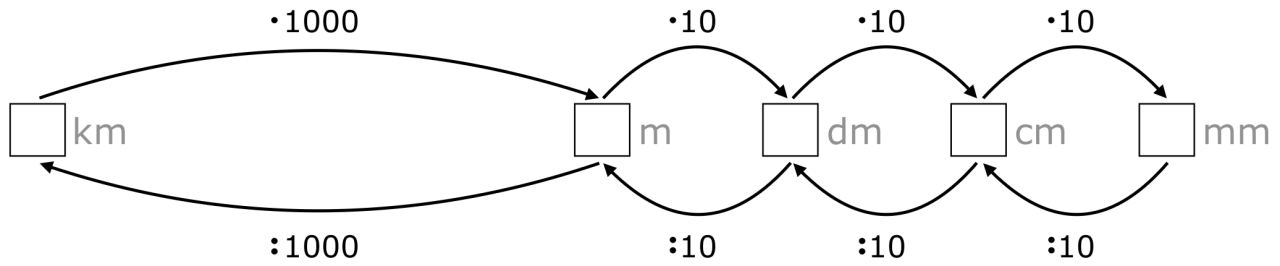 Abbildung 7: Schaubild Umrechnungszahlen (1)
Abbildung 7: Schaubild Umrechnungszahlen (1)
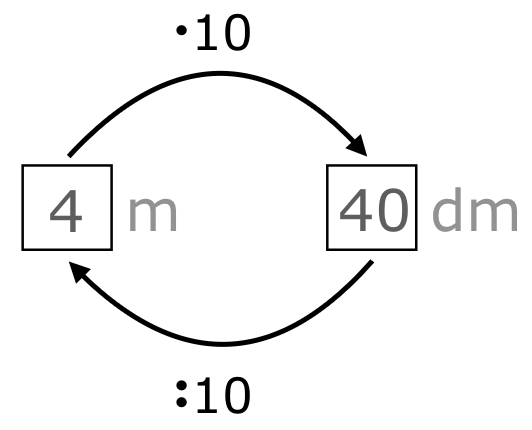 Abbildung 8: Beispiel für die Nutzung des Schaubildes
Abbildung 8: Beispiel für die Nutzung des Schaubildes
Eine Besonderheit stellt die Beziehung zwischen den nicht benachbarten Maßeinheiten m und cm dar, die als einzige derartige Beziehung den meisten Schülerinnen und Schülern bekannt sein dürfte. Diese besondere Beziehung lässt sich mit der zwischen den beiden Maßeinheiten liegenden Maßeinheit Dezimeter (dm) erklären, wie das folgende Schaubild (vgl. Kupsch et al., 2018, S. 91) zeigt.
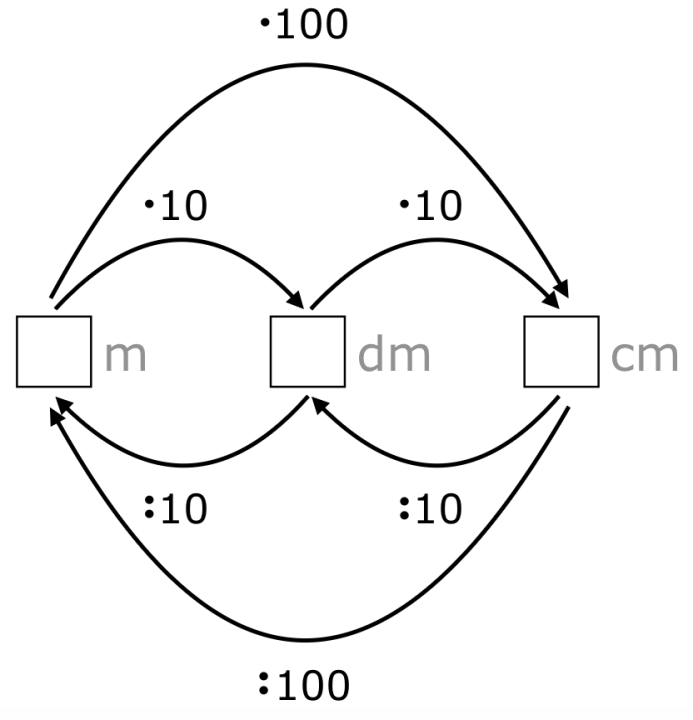 Abbildung 9: Schaubild Umrechnungszahlen (2)
Abbildung 9: Schaubild Umrechnungszahlen (2)
Ausgehend von den oben dargestellten Beziehungen zwischen den Maßeinheiten lassen sich, analog zu dem Vorgehen bei der Beziehung zwischen den Maßeinheiten m und cm, nun alle weiteren Beziehungen zwischen den verschiedenen Maßeinheiten durch die Multiplikation der jeweiligen Umrechnungszahlen berechnen.