Gemeinsames Lernen mit Hilfe niveaudifferenzierter Aufgaben – Das Erforschen des Kommutativgesetzes der Multiplikation auf unterschiedlichen Anforderungsbereichen
Ein konkretes Beispiel für Aufgaben, die die Anforderungsbereiche berücksichtigen entstammt einer Unterrichtsreihe zur Multiplikation („Wir erforschen besondere Mal-Aufgaben“), die in einer aus 30 Schülerinnen und Schülern bestehenden zweiten Schulklasse mit sehr heterogenen Lernvoraussetzungen durchgeführt wurde. In der inklusiven Lerngruppe befinden sich u.a. Kinder mit erhöhtem Unterstützungsbedarf im Bereich „Lernen“ und sonderpädagogischem Unterstützungsbedarf im „sozial-emotionalen Bereich“ sowie im Bereich „Sprache“. Die Klasse weist einen hohen Anteil von Kindern auf, die Deutsch als Zweitsprache lernen.
Das Kernanliegen (der initiierte/bewusste Lernzuwachs) der Unterrichtsreihe bestand darin, die Schülerinnen und Schüler möglichst selbst entdeckend Strukturmerkmale von Multiplikationsaufgaben erforschen zu lassen, wobei ein Operationsverständnis der Multiplikation vorausgesetzt wurde. Ein wesentlicher Bestandteil war dann die Erkenntnis der Gültigkeit des Kommutativgesetzes der Multiplikation, welche durch die Untersuchung verschiedener Aufgabentypen induziert werden sollte. Die gemachten Erkenntnisse sollten den Schülerinnen und Schülern anschließend dazu verhelfen, über verschiedene Strategien zur Lösung von Multiplikationsaufgaben zu verfügen und die strukturellen Zusammenhänge zu verstehen, wodurch eine Grundlage für das Verständnis der Rechenoperation geschaffen werden konnte.
Die hier gezeigten Kinderdokumente sind der Untereinheit „Tauschaufgaben“ entnommen, deren wesentliches Ziel darin bestand, die Kinder die Ergebnisgleichheit von Tauschaufgaben erkennen und eine Begründung für diesen Sachverhalt entwickeln zu lassen. Um die strukturellen Zusammenhänge des Kommutativgesetzes besser fassen und den Kindern einen besseren Zugang zur Verallgemeinerung geben zu können, wurde auf die Nutzung des Hunderterfeldes (Wittmann & Müller, 1993) verwiesen. Wie dieses Kernanliegen für Schülerinnen und Schüler jeden Leistungsniveaus auf allen Anforderungsbereichen erreicht werden konnte, zeigt die exemplarische Erläuterung am folgenden Arbeitsblatt:
 Abbildung 3: Arbeitsblatt „Tauschaufgaben 1"
Abbildung 3: Arbeitsblatt „Tauschaufgaben 1"
Die Aufgaben sind so gestellt, dass Kinder auf allen Anforderungsbereichen arbeiten können:
Anforderungsbereich I
In diesem Beispiel wird der Anforderungsbereich „Reproduzieren“ durch die Lösung der Multiplikationsaufgaben angesprochen. Im Unterricht schafften dies alle Schülerinnen und Schüler. Das ist unter anderem auf die Auswahl der Multiplikationsaufgaben zurückzuführen, die lediglich den Zahlenraum bis 20 abdecken. Um stärkere Kinder nicht zu unterfordern, kann auf ein differenziertes Arbeitsblatt zurückgegriffen werden (vgl. Arbeitsblätter Tauschaufgaben in versch. Differenzierungsstufen). Die Aufgaben sind schwieriger (vgl. ‚Verwandte Aufgaben‘) und zum Teil selbst herauszufinden. Die zu beschreibenden Merkmale sind aber dieselben, sodass die gemachten Entdeckungen im Plenum ausgetauscht werden können.
Anforderungsbereich II
Auch die Teilaufgaben des Anforderungsbereichs „Zusammenhänge herstellen“ wurden von nahezu jedem Kind bearbeitet. Die Aufgabenstellung „Was fällt dir auf?“ machte dies möglich. Sie ist offen gestellt (vgl. ‚Offene Aufgaben‘) und erlaubte es allen Schülerinnen und Schülern, nach Auffälligkeiten zu forschen. Statt einer einzigen, „richtigen“ Lösung gibt es vielfältige Lösungsmöglichkeiten. Zudem wird durch den Hinweis, Forschermittel (vgl. PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Unterrichtsmaterial – Forschermittel-Plakat, s. auch ‚Forschermittel') nutzen zu können, ein differenziertes Bearbeiten gewährleistet, was insbesondere sprachlich schwächeren Kindern dazu verhalf, ihre Entdeckungen kenntlich zu machen. So waren fast alle Kinder dazu in der Lage, das gleiche Ergebnis von Tauschaufgaben mit dem Forschermittel „Farben“ (vgl. PIKAS: Haus 1: Entdecken, Beschreiben, Begründen – Unterrichtsmaterial – Forschermittelplakat) zu verdeutlichen (Abb. 4).
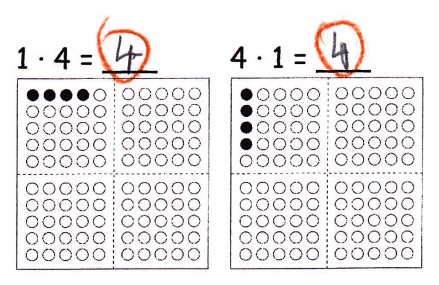 Abbildung 4
Abbildung 4
Unter den Bearbeitungen der Kinder, die sich schriftlich zu ihren Entdeckungen äußerten, gab es eine Bandbreite an Lösungen (Abb. 5; Abb. 6).
 Abbildung 5
Abbildung 5
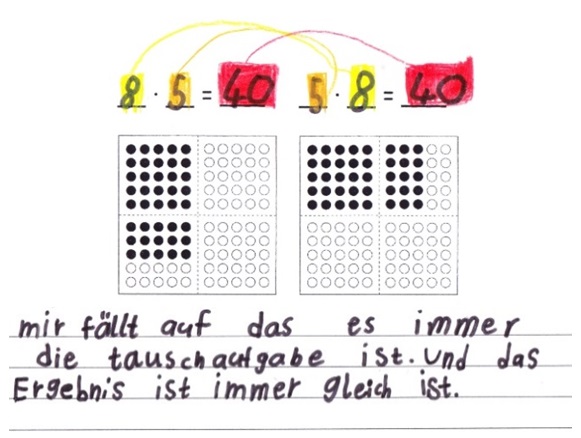 Abbildung 6
Abbildung 6
Anforderungsbereich III
Die Aufgabenstellung „Warum ist das so? Begründe.“ sollte den Lernenden einen Impuls geben, ihre strukturellen Entdeckungen zu begründen (Anforderungsbereich „Verallgemeinern und Reflektieren“). Dies gelang nur den leistungsstarken Schülerinnen und Schülern. Trotzdem haben in der praktischen Durchführung fast alle Kinder versucht, diese Frage zu beantworten. Im Wesentlichen beschrieben sie dabei erneut ihre gemachten Entdeckungen aus Aufgabe 2, was zu einer Verinnerlichung ihrer Entdeckungen und zu einer verständlicheren Artikulation führte (Abb. 7).
 Abbildung 7
Abbildung 7
Leistungsstarke Kinder versuchten, ihre Ergebnisse in Aufgabe 3 zu verallgemeinern. Ihre Begründungsversuche wiesen dabei eine Vielfalt an Lösungsmöglichkeiten auf (Abb. 8; Abb. 9) und zeigen, dass sie während der Bearbeitungszeit mit der Suche nach einer Begründung nicht unterfordert wurden.
 Abbildung 8
Abbildung 8
 Abbildung 9
Abbildung 9
Auf Grundlage der gesammelten Erkenntnisse, die durch Präsentationen der Lernenden erfolgten, wurde abschließend gemeinsam noch näher auf die Begründung des Sachverhaltes eingegangen. Auf ausgeschnittenen Punktefeldern im Großformat (vgl. Anschauungsmaterial „Punktefelder groß") konnte im Plenum der Beweis erfolgen, dass sich die Anzahl der Punkte bei Tauschaufgaben nicht ändert. So konnten die leistungsstärkeren Kinder ihre zuvor verschriftlichten Begründungen (Abb. 10) den anderen Schülerinnen und Schülern mit Hilfe des Anschauungsmaterials erklären.
 Abbildung 10
Abbildung 10
Um die Erkenntnisse der Stunde an einem anderen Darstellungsmittel deutlich zu machen, wurden in der Folgestunde ausgehend von einer Zielzahl (dem Ergebnis) gleich große Sprünge auf dem Rechenstrich (vgl. Arbeitsblätter „Rechenstrich“) vollzogen. Anhand der gefundenen Rechenaufgaben konnten Tauschaufgaben identifiziert und nochmals auf ihre Ergebnisgleichheit eingegangen werden.
Aufgrund der großen Heterogenität in inklusiven Lerngruppen sind in den meisten Fällen noch weitere Differenzierungs- und Unterstützungsmaßnahmen für leistungsschwächere und leistungsstärkere Kinder sinnvoll (vgl. ,Planung von Förderung'). Dabei ist zu bedenken, wie auch Kindern mit Unterstützungsbedarf ein Bearbeiten der Aufträge auf allen Anforderungsbereichen ermöglicht werden kann (vgl. ‚Tipps und Herausforderungen‘).
Weitere Anregungen
An die hier erläuterte Untereinheit „Tauschaufgaben“ lassen sich Einheiten zu „Kern-“ und „Quadratzahlaufgaben“ sinnvoll anknüpfen (vgl. Arbeitsblätter „Quadratzahlaufgaben“). Letzteres bietet sich vor allem dann an, wenn bereits im Vorfeld in einer anderen Unterrichtsreihe die Eigenschaften eines Quadrates thematisiert wurden. Die Übertragbarkeit dieser Eigenschaften auf Quadratzahlen kann auch bei Schülerinnen und Schülern mit Schwierigkeiten im arithmetischen Bereich dazu führen, strukturelle Erkenntnisse hinsichtlich von Multiplikationsaufgaben zu gewinnen. Die Aufgabenstellungen dieses Arbeitsblattes sind ebenfalls so gewählt, dass sie die zuvor erläuterten Anforderungsbereiche berücksichtigen, so dass alle Lernenden die Möglichkeit haben, die Aufgaben auf ihrem Niveau zu lösen.