Nach der Auseinandersetzung mit verschiedenen Testverfahren entscheidet sich Carlas Klassenlehrer für den Einsatz des Bielefelder Rechentests für das zweite Schuljahr. Im Folgenden werden die Auswahlkriterien für diesen Test und dessen Einsatz beispielhaft konkretisiert.
Entscheidung für einen unterrichtsrelevanten Test
Der Bielefelder Rechentest erfüllt die im „Hintergrund“ aufgeführten Auswahlkriterien wie folgt:
-
Zielsetzung: Förderdiagnostik à objektive und differenzierte Einschätzung arithmetische Basiskompetenzen und Entwicklung darauf aufbauender Förderplanung
-
Ausrichtung: Schwerpunkt Prozessorientierung à Aufstellung von Hypothesen über das Vorhandensein von Symptomen für Rechenschwierigkeiten durch Zeit- und Fehleranalysen/ Kopplung mit Hinweisen zur weiteren prozessorientierten Diagnose im Einzelgespräch
-
Grad der Standardisierung und Normierung: standardisiert/ Normstichprobe von über 2000 Kindern
-
Themenbereiche:
-
sichere Orientierung in den Zahlenraum 20 bis 100
-
arithmetische Basiskompetenzen, wie schnelle Zahlauffassung, Zahlzerlegung etc.
-
sicheres Addieren und Subtrahieren im Zahlenraum bis 100 und Nutzung von Aufgabenbeziehungen
-
Größen und Grundvorstellungen
-
Altersstufe:
-
Lernende des zweiten Schuljahres, hier insbesondere differenziert für schwächere Rechner
-
Einsatz auch möglich in höheren Altersstufen mit Anpassung an die jeweiligen individuellen Kompetenzen
-
Dauer: in Anpassung an das Lerntempo der Lernenden, Unterbrechungen sind möglich/ im Schnitt werden ein bis zwei Schulstunden benötigt
-
Durchführung:
-
einsetzbar als Gruppen- oder Einzeltest
-
selbständige Bearbeitung durch die Lernenden am Computer, eine Sprachausgabe liefert notwendige Erklärungen
-
konkrete praktische Hinweise zu weiteren prozessorientierten Diagnostik im beiliegenden Handbuch
-
Auswertung:
-
Auswertung der Daten durch das Programm
-
als Ausdruck: zusammenfassende Bewertung von Schülerleistungen, Vergleich derselben mit der Normierungsstichprobe, Zeit- und Fehleranalysen, Einschätzung der Arbeitsweise
-
Materialeinsatz:
-
Computer
-
gegebenenfalls Kopfhörer für die Sprachausgabe
-
gegebenenfalls gängiges fachdidaktisches Material bei weiterer Diagnose mit dem Handbuch (z.B. Wendeplättchen, Rechenrahmen etc.)
-
Sprachliche Anforderungen: arithmetisches Basisvokabular des zweiten Schuljahres im passiven Wortschatz
-
Kombination mit Förderhinweisen: konkrete und praxisnahe Anleitung zur gezielten Förderung kritischer Bereiche im beiliegenden Handbuch
Tipp:
Ein leeres Formular mit den aufgeführten Auswahlkriterien für eigene Einschätzungen von Diagnoseinstrumenten steht im
Materialteil zur Verfügung!
Verschiedene Gründe sprechen aus der Sicht von Carlas Klassenlehrer für den Einsatz des Bielefelder Rechentests:
-
Die möglichen kritischen Stellen im arithmetischen Verständnis zu diesem Zeitpunkt des Lernens werden durch das computerbasierte Verfahren genauer abgeklärt.
-
Durch die Verbindung mit weiteren Diagnoseschritten aus dem Handbuch lässt sich die Diagnostik passgenau und individuell gestalten. Der Lehrer erhält ein differenziertes Abbild der Lernausgangslage im Bereich Arithmetik, in welchem die Schülerin derzeit die größten Schwierigkeiten zeigt.
-
Darüber hinaus werden konkrete und praktikable Fördermöglichkeiten aufgezeigt, welche sich direkt an die Diagnostik anschließen. Insbesondere Letzteres ist für Carlas Klassenlehrer eine wertvolle Unterstützung, da er Mathematik – wie erwähnt - fachfremd unterrichtet.
Durchführung der Diagnostik
Nach der Entscheidung für den Bielefelder Rechentest legt der Klassenlehrer fest, diesen mit Carla in einer ruhigen Einzelsituation durchzuführen. Somit soll ihr die Fokussierung auf die Anforderungen desselben erleichtert werden. Nach der Installation des Programms wird sie mit Geburtsdatum eingetragen und kann mit dem Test beginnen. Erläuterungen inhaltlicher Art dürfen von der Lehrkraft nicht gegeben werden, sondern erfolgen allein durch das Programm selbst, um die Vergleichbarkeit mit der Normierungsstichprobe gewährleisten zu können. Carla kann somit selbstständig und ohne ständige Präsenz ihres Lehrers den Test bearbeiten. Insgesamt sind maximal 60 Minuten Zeitaufwand geplant.
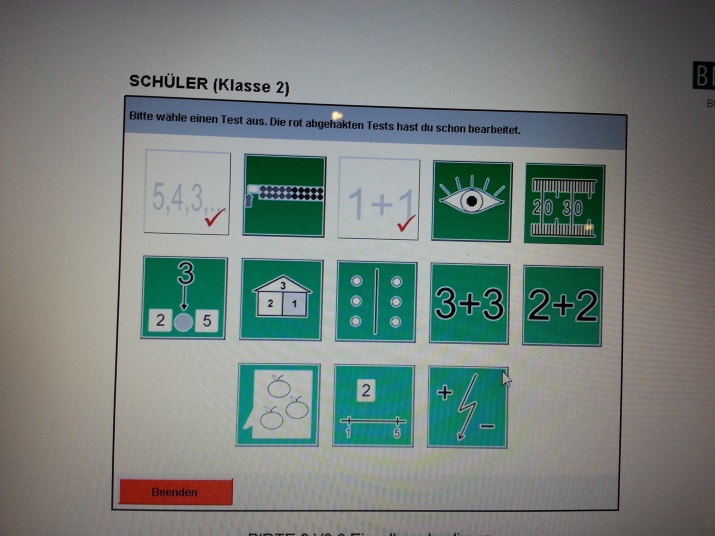Abbildung 2: Bildschirmausschnitt mit der Übersicht der Untertests für die Lernenden
Da bei der Durchführung immer wieder auffällt, dass Carlas Konzentration nachlässt, wird die Testung auf mehrere Tage verteilt. Somit möchte der Klassenlehrer ein genaueres Bild über ihre eigentlichen mathematischen Fähigkeiten erhalten.
Auswertung der Diagnostik
Die Auswertung erfolgt im Anschluss automatisch durch das Computerprogramm und steht dem Lehrer als Ausdruck zur Verfügung.
Im Folgenden werden beispielhaft einige Ergebnisse der computerbasierten Testauswertung von Carla gezeigt (hier als „Schüler“ bezeichnet).
Abbildung 3: Ausschnitt aus den Testergebnissen von Carla
„Zusammenfassung“ und „Auffällige Module“
Im Anschluss an die zusammenfassende Übersicht der Testergebnisse wird die Bearbeitung der einzelnen Modulgruppen detailliert dargestellt und erläutert. Im Weiteren sind Auszüge aus Carlas Ergebnissen bezüglich der im Einstieg dargelegten Zahlendreher und dem dort gezeigten Rechnen beispielhaft einzusehen:
Abbildung 4: Ausschnitt aus den Testergebnissen von Carla
Modulgruppe „Orientierung im Zahlenraum“ / Beispiel zu „Zahlendrehern“
Abbildung 5: Ausschnitt aus den Testergebnissen von Carla
Modulgruppe „Rechnen“ – Beispiel
Zur Interpretation dieser Testergebnisse sind darüber hinaus folgende Informationen aus dem „Quantitativen Befund“ aufschlussreich, da sie zeigen, wie wichtig eine sich anschließende individuellere, auf Carla zugeschnittene Diagnostik ist.
Abbildung 6: Ausschnitt aus den Testergebnissen von Carla
„Quantitativer Befund“
Aus den Resultaten lassen sich zu diesem Zeitpunkt folgende vorläufige Schlüsse bezüglich Carlas Lernstand im Bereich Arithmetik ziehen:
-
Es zeigt sich, dass die im Einstieg beschriebenen Zahlendreher tatsächlich eine Schwierigkeit darstellen, aber offenbar nur ein problematischer Bereich von mehreren zu sein scheinen. Die Vermutung des Klassenlehrers wird folglich durch die Testergebnisse bestärkt.
-
Am Beispiel Rechnen wird deutlich, wie weitreichend die kritischen Bereiche scheinbar sind. Als Hypothese formuliert der Test die Möglichkeit, dass Carla zu den zählenden Rechnern gehört und eine umfassendere Förderung nötig sein könnte. Es wird dringend empfohlen, mit Hilfe des Handbuchs eine gezieltere Diagnostik dahingehend durchzuführen.
-
Die Testauswertung hebt darüber hinaus Carlas besondere Arbeitsweise hervor („mit wenig Sorgfalt“, war eventuell „mit dem Test überfordert“, s. Abb. 6). An dieser Stelle zeigt sich, dass standardisierte Testverfahren zwar ihre Grenzen haben, aber durch informelle individuelle Diagnosen fortgeführt und vertieft werden können.
Im Bielefelder Rechentest wird dem Klassenlehrer eine nächste konkrete Handlungsoption eröffnet:
Unter den angegebenen Kapitelverweisen erhält er jeweils eine praktische Anleitung zur weiteren prozessorientierten, individuellen Diagnose. Hierfür schlägt der Test verschiedene Diagnoseaufgaben, insbesondere aus den Bereichen Zahlzerlegungen, Zehnerübergang beim Rechnen (Rechnen mit vollen Zehnern, Rechnen mit Zehnern und Einern) sowie Aufgabenbeziehungen und Rechenstrategien (Tausch- und Umkehraufgaben, Analogien, flexibles Rechnen) vor. Darüber hinaus wird angeregt, dass aufgrund der gemachten Zahlendreher auch das Schreiben und Lesen von Zahlen genauer betrachtet werden sollte.
Weiterführende individuelle Diagnostik
Die weiteren Diagnoseschritte in Anlehnung an die Vorschläge des Handbuchs werden an anhand des Beispielbereichs „Schreiben und Lesen von Zahlen“ näher skizziert (vgl. Schipper, Wartha & von Schroeders, 2013).
Zunächst beschreibt das Handbuch die diesbezüglich typischen Hürden.
Die Sprechweise der Zahlwörter 13 bis 99 entspricht im Deutschen nicht der üblichen Schreibrichtung von links nach rechts. Diese Diskrepanz kann zu Problemen führen, insbesondere wenn der Tipp gegeben wird, die Zahlen so in umgekehrter Richtung zu schreiben, wie man sie spricht (invers). Die Schwierigkeiten der Übersetzung können sich nicht nur beim Schreiben von Zahlen zeigen, sondern auch beim Darstellen mit Material und beim Lesen von Zahlen. Es ergeben sich die hierfür typischen Zahlendreher und gegebenenfalls Beeinträchtigungen beim Erwerb des Stellenwertverständnisses.
Im Anschluss an die kurzen Ausführungen werden verschiedene Beobachtungsschwerpunkte und möglichen Diagnoseaufgaben aufgelistet. Unter diesen wählt Carlas Klassenlehrer einige aus, welche ohne großen Aufwand und mit den üblichen, der Klasse zur Verfügung stehenden Materialien umzusetzen sind:
Diagnoseaufgaben:
-
Zahlendiktat
-
Zahlen laut vorlesen lassen
-
Zahlen mit Material darstellen (Zahlen mit Zehnerstangen und Einerwürfeln legen / Zahlen in der Stellenwerttafel darstellen)
Beobachtungsschwerpunkte:
-
Schreibt Carla Zahlen invers, notiert sie also erst die Einer, dann die Zehner links davon?
-
Kommen auch beim Lesen Zahlendreher vor? Entstehen beim Lesen von Zahlen Pausen, die auf eine besondere Irritation schließen lassen?
-
Werden beim Darstellen von Zahlen mit Material die entsprechenden Zahlendreher dargestellt?
Tipp:
Unterstützt werden kann dieser individuelle Diagnoseschritt durch Einsatz des
Leitfadens zum Führen von Diagnosegesprächen!
Die folgenden Abbildungen zeigen einige von Carlas Ergebnissen:
Zahlendiktat: Diktiert werden die Zahlen 15, 20, 23, 34, etc.
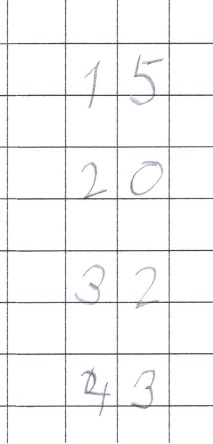Abbildung 7: Notationen im Zahlendiktat
Hier fällt auf, dass Carla die Zahlen 15 und 20 adäquat notiert, ihr bei den Zahlen 23 und 34 jedoch Zahlendreher unterlaufen.
Ergänzt werden kann hier das Dokument durch die Beobachtung des Lehrers, dass insbesondere bei den letztgenannten Zahlen eine kleine Pause entsteht, in welcher Carla nachdenkt, unschlüssig mit dem Stift über dem Blatt verweilt und dann zu schreiben anfängt. Hier liegt die Vermutung nahe, dass Carla die Schreibweise der Zahlen aus dem schon seit dem ersten Schuljahr bekannten Zahlenraum auswendig abgespeichert hat. Sobald es darüber hinausgeht, zeigt sich eine deutliche Unsicherheit beim Schreiben. Diese wird auch beim anschließenden Vorlesen der Zahlen deutlich: Während 15 und 20 flüssig gelesen werden, wird Carla danach sehr unsicher.
Aufschlussreich ist darüber hinaus das anschließende Legen der Zahlen mit Material:
Abbildung 8: Darstellungen von Carla mit Dienes - Material
Hierbei fällt sofort auf, dass die Zahl 23 adäquat gelegt wurde, während 34 wiederholt einen Zahlendreher aufweist. Die Beobachtung Carlas liefert dazu folgende Zusatzinformation: Im Anschluss an die korrekt gelegte 20 wird Carla aufgefordert, die 23 zu legen. Ihr Blick geht sofort vor der Auswahl des benötigten Materials zur bereits gelegten 20. Sie überlegt und greift zwei Zehnerstangen, dabei immer noch im Blickkontakt mit der korrekten Darstellung der 20. Sie fragt nochmal nach, welche Zahl sie legen soll, legt beide Zehnerstangen und wählt korrekt drei Einerwürfel, welche sie rechts neben die beiden Zehnerstangen platziert. Bei der anschließend diktierten 34 überlegt sie kurz und legt oben zu sehende 43.
Diese Ergebnisse untermauern nochmals die Vermutung, dass Carla deutliche Unsicherheiten bei den Übersetzungsprozessen zwischen sprachlicher und symbolischer Ebene in Form des Schreibens von Zahlen sowie der Darstellung von Zahlen im Stellenwertsystem hat. Somit sind die regelmäßigen Zahlendreher nicht lediglich auf eine inverse Schreibweise oder Herausforderungen im sprachlichen Bereich zurückzuführen. Hier sollte eine anschließende Förderung umfassend anknüpfen.
Tipp:
Unterstützt werden kann der diesbezügliche Planungsprozess durch den Einsatz des
Formular zur Planung von individueller Förderung!
Ansätze der Förderung
Auf der Diagnostik aufbauende Förderansätze werden im Handbuch ebenfalls konkret angeleitet (vgl. Schipper, Wartha & von Schroeders, 2013). Ziel von Carlas Förderung bezüglich der Zahlendreher ist aufgrund des Gesamtergebnisses unter anderem eine Sicherung des Stellenwertverständnisses, welche an folgender Übung mit Hilfe von Dienes - Material und Stellenwerttafel in Anlehnung an das Vierphasenmodell konkretisiert werden soll:
Tipp:
Erläuterungen zum Vierphasenmodell finden Sie unter "Diagnose- und Fördergespräche: Unterricht"und bei PIKAS: Vierphasenmodell.
Phase 1: Handlung am Material: Eine Zahl wird genannt, Carla fordert die benötigten Zehnerstangen und Einerwürfel an und legt sie links (Zehner) und rechts (Einer) nebeneinander. Im Anschluss wird in dieser korrekten Reihenfolge die Zahl zunächst in die Stellenwerttafel notiert, danach als Ziffernfolge (siehe Abbildung 9).
Phase 2: Handlung mit Sicht auf das Material: Im nächsten Schritt führt die Lehrkraft die obigen Schritte nach den Handlungsanweisungen Carlas aus, während diese ihr Vorgehen kontrolliert.
Phase 3: Ohne direkte Sicht auf das Material: Im nächsten Schritt führt die Lehrkraft die Schritte nach den Handlungsanweisungen Carlas aus, währenddessen das Material mit einer Sichtbarriere durchgehend verdeckt ist. Die Kontrolle erfolgt im Anschluss gemeinsam mit Sicht auf das Material.
Phase 4: Handlung ohne Material: Alle Schritte werden in der Vorstellung durchgeführt und verbalisiert. Zweistellige Zahlen werden direkt notiert.
Abbildung 9: Fördermaterialien
Die beschriebenen Übungen setzt Carlas Klassenlehrer sowohl in einer Einzelsituation als auch in Partnerarbeiten und in der täglichen „Mathe - Blitzrunde“ im Plenum innerhalb der Klasse ein. Vorteil bei den letzteren beiden Organisationsformen ist die Einforderung von Übersetzungsprozessen zwischen den Repräsentationsebenen von allen Lernenden zur Sicherung der Darstellung von Zahlen im Stellenwertsystem. Diese Übungen zu den Übersetzungsprozessen werden für sehr starke Rechner als „verwandte Aufgabe“ (vgl. ‚Verwandte Aufgaben’) auch immer wieder über den Zahlenraum bis 100 hinausgehend umgesetzt.
Die weitere Förderung Carlas, welche gemäß der dargestellten Testergebnisse in weiteren Bereichen (unter anderem Zahlzerlegungen, Rechnen mit Zehnerübergang, Rechenstrategien) umfangreicher ausfällt, wird im Anschluss mit Hilfe des Handbuchs evaluiert, indem einzelne Diagnoseaufgaben mit Carla zu einem späteren Zeitpunkt wiederholt durchgeführt werden.
Somit unterstützt der Bielefelder Rechentest im aufgezeigten Beispiel handlungsleitend auch die Planung und Durchführung der Förderung von Carla.
Weitere Anregungen
In der weiteren Förderung setzt Carlas Klassenlehrer ein Blitzblick-Quartett ein. Hiermit kann der Darstellungswechsel zwischen Symbol, Zahlwort, Mengendarstellung am Rechenrahmen und mit Dienes – Material gefördert werden, beispielsweise durch die Zuordnung einzelner Karten in Einzelarbeit oder als Partnerübung.
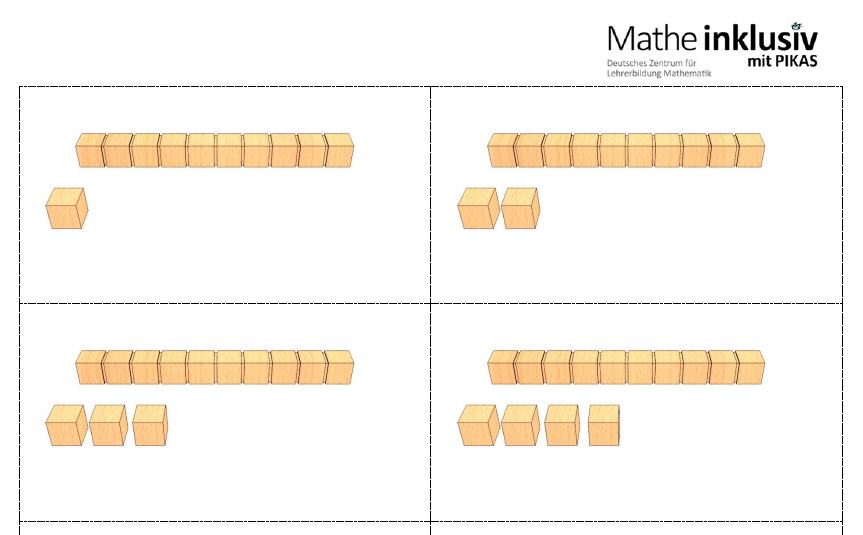Abbildungen 10 und 11:
Beispiele für Karten aus dem Blitzblick - Quartett bis 20
Das Video zeigt beispielhaft einen Ausschnitt aus einer Fördereinheit mit dem Blitzblick – Quartett mit der zuständigen Sonderpädagogin.
Tipp:
Im Materialteil stehen sowohl ein Quartett für den Zahlenraum bis 20 als auch bis 100 zur Verfügung, ergänzt durch eine beispielhafte Planung einer Fördereinheit. Individuell können die Karten von der Lehrkraft ergänzt oder auch nur in Teilen eingesetzt werden und ermöglichen ein Arbeiten in unterschiedlichen Zahlenräumen für alle Lernenden eines zweiten Schuljahres.
