Für einen Gesamtüberblick werden nachfolgend die verschiedenen Verfahren der schriftlichen Subtraktion vorgestellt. Insgesamt können für die schriftliche Subtraktion fünf Verfahren genutzt werden: Das Abziehen mit Entbündeln, das Ergänzen mit Entbündeln, das Abziehen mit Erweitern, das Ergänzen mit Erweitern und das Ergänzen mit Auffüllen bzw. Bündeln.
Die Verfahren unterscheiden sich zum einen mit Blick auf die Rechenrichtung und zum anderen im Umgang mit dem Übertrag (wenn denn ein Übertrag vorgenommen werden muss).
Zur Veranschaulichung der Handlungsschritte bei der Erarbeitung und Vertiefung der Subtraktionsverfahren können im Unterricht unter anderem Legematerial wie Mehrsystemblöcke oder Hunderterpunktefelder, Zehnerstreifen und Wendeplättchen verwendet werden (s. auch Ziffernrechnen: Unterricht).
Die fünf Verfahren der schriftlichen Subtraktion im Überblick
Im Folgenden werden die fünf Verfahren der schriftlichen Subtraktion vorgestellt. Dafür werden zunächst die beiden Rechenrichtungen, die bei Subtraktionsaufgaben genutzt werden können, betrachtet: das Abziehen und das Ergänzen.
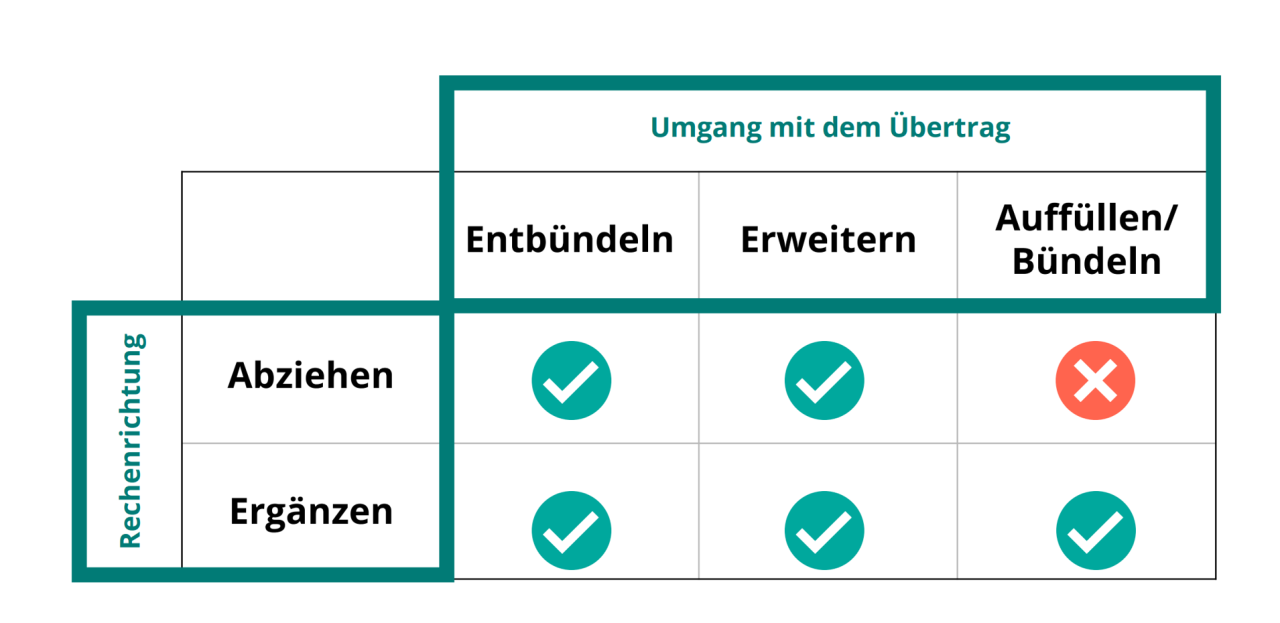Abbildung 1: Die verschiedenen Verfahren der schriftlichen Subtraktion im Überblick
Die zwei Rechenrichtungen im Überblick
Die Rechenrichtung bezieht sich auf die zu aktivierende Grundvorstellung der Subtraktion: Abziehen oder Ergänzen (vgl. Schulz & Wartha, 2021). Diese werden im Folgenden an der Beispielaufgabe 5-3 erläutert.
Abbildung 2: Die zwei Rechenrichtungen Abziehen und Ergänzen anhand von Punkten dargestellt
Beim Abziehen wird die Differenz durch das Wegnehmen des Subtrahenden vom Minuenden bestimmt. In der Abbildung werden von fünf Plättchen drei Plättchen durchgestrichen bzw. abgezogen, also 5-3=2 gerechnet (hier und im Folgenden wird das Wegnehmen immer durch rote Durchstreichungen veranschaulicht). Das Ergebnis dieser Aufgabe ist also das, was übrigbleibt.
Abbildung 3: Die Rechenrichtung Abziehen anhand von Punkten dargestellt
Beim Ergänzen wird die Differenz durch das Ergänzen des Subtrahenden bis zum Minuenden bestimmt. In der Abbildung sind drei Plättchen bereits als Subtrahend ausgelegt. Um die fünf Plättchen (also den Minuenden) zu erhalten, werden zu den drei Plättchen zwei weitere Plättchen hinzugefügt bzw. ergänzt, also 3+2=5 gerechnet (hier und im Folgenden wird das Ergänzte immer grün veranschaulicht). Das Ergebnis dieser Aufgaben ist also das, was dazugelegt wurde.
Abbildung 4: Die Rechenrichtung Ergänzen anhand von Punkten dargestellt
Die drei Umgänge mit den Überträgen im Überblick
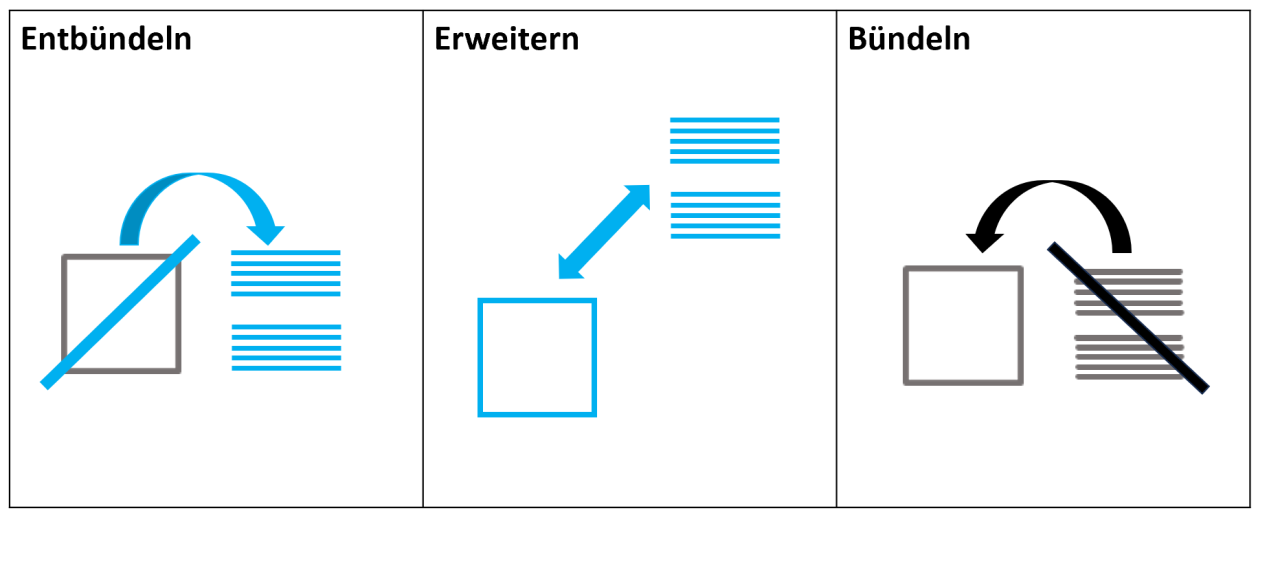Abbildung 5: Entbündeln, Erweitern und Auffüllen/Bündeln beim Übertragen im Überblick
Beim Entbündeln wird nur der Minuend verändert, indem bspw. ein Hunderter zu zehn Zehnern entbündelt wird. Es wird immer der nächstgrößere Stellenwert für den Ausgangsstellenwert entbündelt.
Beim Erweitern werden sowohl Minuend als auch Subtrahend gleichsinnig verändert bzw. erweitert. Dem Minuenden werden bspw. zehn Zehner hinzugefügt, während dem Subtrahenden ein Hunderter hinzugefügt wird, um die Differenz bei der Subtraktion konstant zu halten. In der Abbildung wird das gleichsinnige Verändern um einen Hunderter und zehn Zehner dargestellt.
Beim Bündeln wird der Subtrahend stellenweise so lange ergänzt, bis der Minuend erreicht wird. Wird dabei ein Stellenwert (H, Z, E) überschritten, muss gebündelt werden. Demnach werden zehn Einer zu einem Zehner oder, wie in der Abbildung dargestellt, zehn Zehner zu einem Hunderter gebündelt. Diese Möglichkeit, mit dem Übertrag umzugehen, wird häufig auch „Auffüllen“ genannt (vgl. z. B. Padberg & Benz 2021, S. 264). Da das Wort „Auffüllen“ jedoch eher die Rechenrichtung beschreibt und weniger den Prozess, der beim Übertrag stattfindet, wird im Folgenden auch weiterhin vom Bündeln gesprochen (vgl. Schulz & Wartha 2021, S. 101).
Folgend wird die Vorgehensweise aller Verfahren konkret erläutert. Dabei werden zuerst die in Schulbüchern häufig eingeführten Verfahren Abziehen mit Entbündeln, Ergänzen mit Erweitern und Ergänzen mit Auffüllen bzw. Bündeln vorgestellt. Weniger üblich, aber dennoch möglich, sind die im Anschluss beschriebenen Verfahren des Ergänzens mit Entbündeln und des Abziehens mit Erweitern.
Dabei werden jeweils die schriftliche Notation der Algorithmen, die Sprechweise sowie die Materialhandlung mit Zahlenbildern anhand der Aufgabe 572-149 beschrieben. Zum Aufbau eines tragfähigen Stellenwertverständnisses und zur Veranschaulichung der einzelnen Schritte für die Kinder können ebensolche Zahlenbilder, Mehrsystemblöcke oder Punktefelder und Plättchen genutzt werden (s. dazu auch Stellenwertvorstellungen: Unterricht: Zahlen darstellen).
Um die einzelnen Handlungsschritte im Bild unterscheidbar zu machen, werden im Folgenden unterschiedliche Farben für unterschiedliche Handlungsschritte verwendet: Das Wegnehmen von Einern, Zehnern oder Hundertern wird durch Durchstreichungen in der Farbe Rot dargestellt. Ergänzte Einer, Zehner oder Hunderter werden in der Farbe Grün dargestellt. Das gleichsinnige Verändern und das Entbündeln werden in den Abbildungen in der Farbe Blau dargestellt. Beim Auffüllen bzw. Entbündeln wird keine weitere Farbe genutzt, da sonst die Differenz im Bild nicht mehr sichtbar wäre.
