Brailleschrift
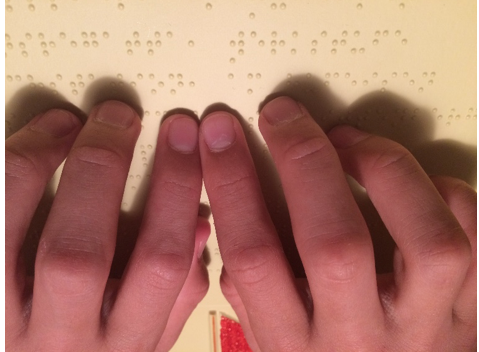 Abbildung 8: Taktiles Erlesen von Brailleschrift
Abbildung 8: Taktiles Erlesen von Brailleschrift
Die Brailleschrift stellt sicherlich das bekannteste Medium der Blindenpädagogik dar. Sie wurde von Louis Braille, der selbst als Kleinkind erblindet ist, 1825 in Frankreich als gut lesbare und einfach zu produzierende taktile Schrift entwickelt. Bis heute ermöglicht die Brailleschrift blinden Menschen die Teilhabe an schriftlicher Kommunikation und schafft vielfältige Informations- und Bildungszugänge. Zu bedenken ist, dass das Lesen der Brailleschrift auch bei geübten Leserinnen und Lesern etwa zwei- bis dreimal langsamer ist als das visuelle Lesen.
 Abbildung 9: Grundraster der Brailleschrift
Abbildung 9: Grundraster der Brailleschrift
Das Grundraster der Brailleschrift besteht aus 6 taktilen Punkten, die in zwei Spalten à drei Punkten angeordnet sind (vgl. Abb. 9): Je nach Anordnung der Punkte lassen sich insgesamt 63 verschiedene Punktschriftzeichen bilden. Dies reicht aus, um sämtliche Buchstaben und Satzzeichen eindeutig zu definieren. Die aus dem französischen Originalsystem für die deutsche Sprache nicht benötigten Sonderzeichen (z.B. é, à) wurden für die deutschen Umlaute ä, ö, ü verwendet und die darüber hinaus noch freien Zeichen für die häufigen Buchstabenkombinationen bzw. Laute ch, sch, au, ei, äu, eu, ie und st. Die Großschreibung wird durch ein vorangestelltes Ankündigungszeichen angezeigt, ebenso die Zifferndarstellung (vgl. Abb. 9 und im Folgenden „Mathematikschrift“).
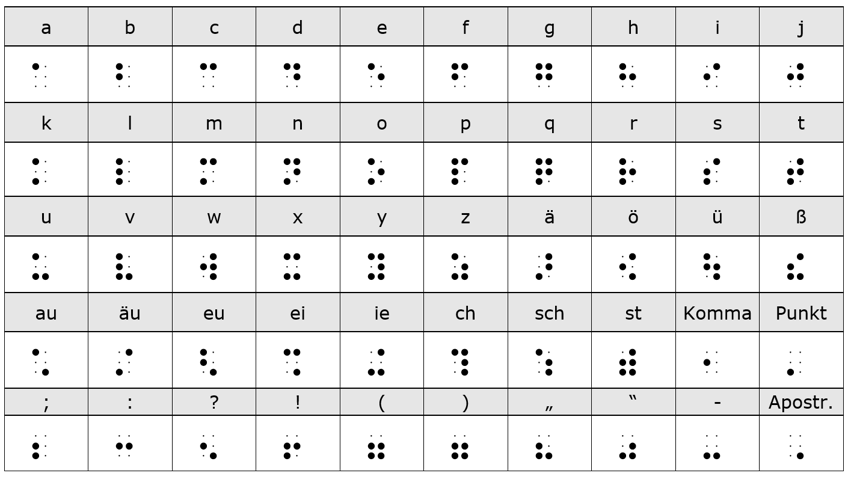 Abbildung 10: Zeichensatz für die deutsche Braille-Schrift
Abbildung 10: Zeichensatz für die deutsche Braille-Schrift
Im Zuge der Computernutzung musste die Sechspunktmatrix erweitert werden, da für eine eindeutige Zeichenzuordnung auch für Großbuchstaben und Ziffern eigene Zeichen benötigt werden. Diese Computer-Brailleschrift besteht aus 8 Punkten (Abb. 10): Die Kleinbuchstaben bleiben in Computerbraille (mit Ausnahme der Umlaute und ß) identisch zur 6-Punktschrift. Die Großschreibung wird mit Hinzufügen des Punktes 7 markiert.
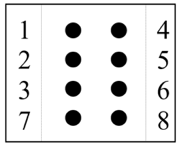 Abbildung 11: Grundraster der Computer-Brailleschrift
Abbildung 11: Grundraster der Computer-Brailleschrift
Kinder mit Blindheit erlernen im Laufe ihrer Schulzeit sowohl die 6-Punktschrift als auch die auf acht Punkte erweiterte Computerschrift. Wird der Computer bereits ab der 1. Klasse eingesetzt, wie z.B. häufig in der schulischen Inklusion, beginnt der Schriftspracherwerb in der Regel mit Computerbraille.
Als weiteres Schriftsystem kommt meist ab der Sekundarstufe 1 die Braille-Kurzschrift hinzu. Diese Kurzschrift wurde entwickelt, um den großen Platzbedarf beim Ausdrucken der Brailleschrift auf Papier zu verringern. Die Braille-Kurzschrift umfasst ein komplexes Regelwerk, das Lautgruppen-, Wort- und Wortstammkürzungen ausweist (Brailleschriftkommission der deutschsprachigen Länder, 2018). Einige Beispiele können die verschiedenen Kürzungsprinzipien verdeutlichen:
 Abbildung 12: Beispiele für Kürzungsprinzipien der Braille-Kurzschrift
Abbildung 12: Beispiele für Kürzungsprinzipien der Braille-Kurzschrift
Mathematikschrift
Für das Notieren mathematischer Ausdrücke existieren wie im literarischen Kontext die 6-Punktschrift und insbesondere für die Computeranwendung die aus 8 Punkten bestehende Computerschrift. Grundsätzlich müssen mathematische Ausdrücke in Brailleschrift streng linear angeordnet werden, da es – z.B. zur Darstellung von Brüchen oder Quadratzahlen – keine verschiedenen Schreibebenen gibt.
Um in der traditionellen 6-Punktdarstellung Buchstaben von Ziffern unterscheiden zu können, muss bei der Zifferndarstellung ein entsprechendes Ankündigungszeichen (Zahlzeichen: Punkte 3, 4, 5, 6) vorangestellt werden. Durch diese Ankündigung wird beispielsweise aus dem Buchstaben "a" die Ziffer 1.
In Computerbraille bestehen genügend Punktkombinationen, um allen Ziffern eindeutig definierte Braillezeichen zuordnen zu können. In Abbildung 13 werden einige mathematische Notierungen beispielhaft veranschaulicht (Leuders & Lang, im Druck).
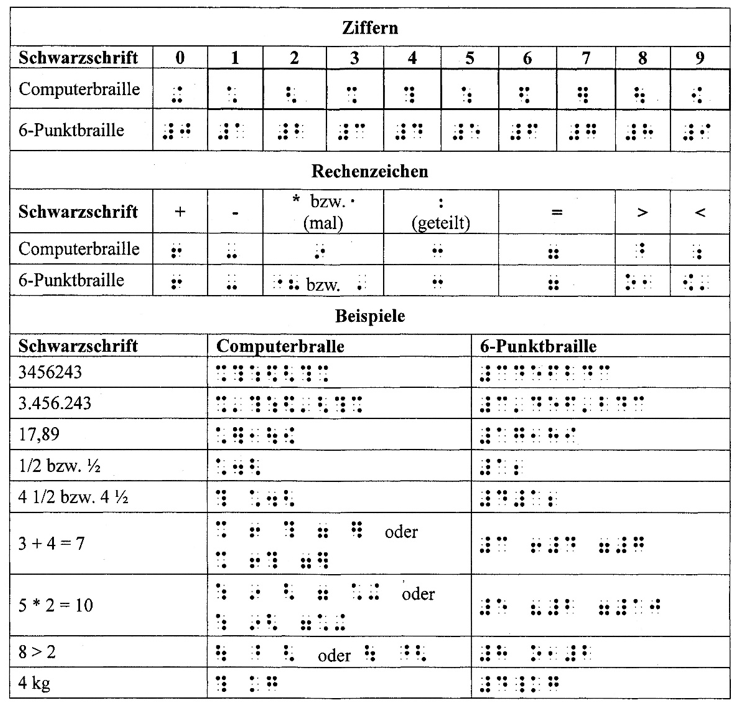 Abbildung 13: Beispielhafte mathematische Notierungen
Abbildung 13: Beispielhafte mathematische Notierungen